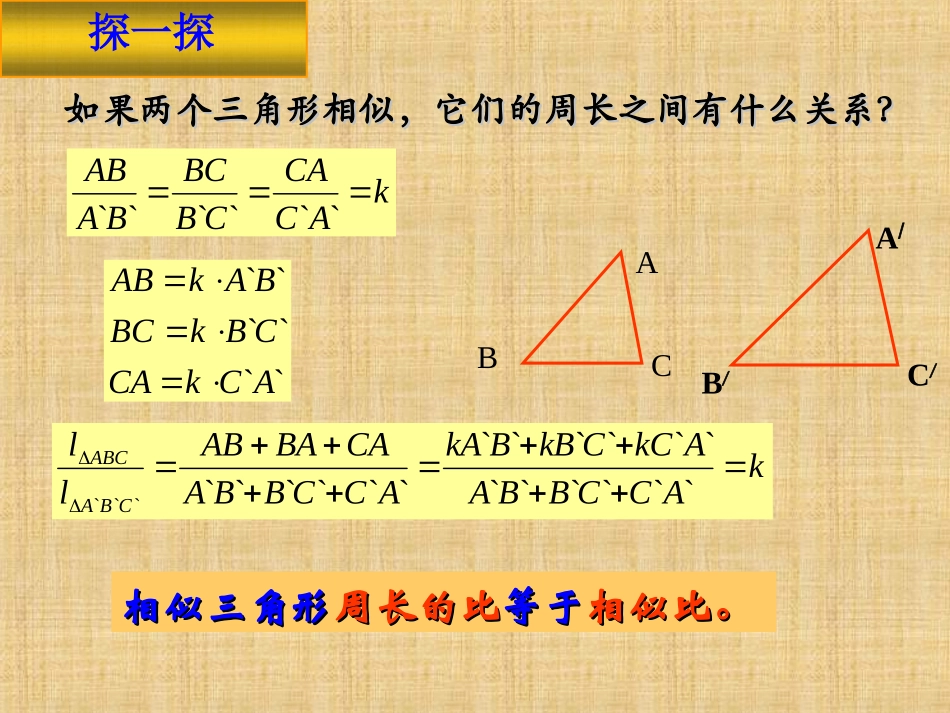
(2)相似三角形有什么性质?对应角相等,对应边成比例;(3)相似三角形的对应边的比叫什么?相似比(4)ΔABC与ΔA/B/C/的相似比为k,则ΔA/B/C/与ΔABC的相似比是多少?1k(1)相似三角形有哪些判定方法?定义,定理,(SSS),(SAS),(AA),(HL)温故知新如果两个三角形相似,它们的周长之间有什么关系?如果两个三角形相似,它们的周长之间有什么关系?ABCA/B/C/相似三角形相似三角形周长的比周长的比等于等于相似比。相似比。kACCACBBCBAAB````````````ACkCACBkBCBAkABkACCBBAAkCCkBBkAACCBBACABAABllCBAABC`````````````````````探一探六边形ABCDEF∽六边形A1B1C1D1E1F1,且相似比是k。BCDEFAB1C1D1E1F1A111111111111111111111111111111.1..ABBCCDDEEFFAkABBCCDDEEFFAABBCCDDEEFFAkABBCCDDEEFFAABCDEFkABCDEF等比六边形的周长六边形的周长相似多边形周长的比等于相似比。三角形中,除了角和边外,还有三种主要线段:三角形中,除了角和边外,还有三种主要线段:高线,角平分线,中线高线,角平分线,中线高线角平分线中线想一想相似三角形的相似比与对应边上高线比有什么关系?相似三角形的相似比与对应边上高线比有什么关系?例如:ΔABCΔA∽/B/C/,ADBC于D,A/D/B/C/于D/,求证:''''ADABkADABABCDA/B/C/D/①①相似三角形的相似三角形的对应高线之比对应高线之比等于等于相似比。相似比。思考ADA′D′ABA′B′∴______==K证明: △ABCA′B′C′∽△∴∠B=B′∠又 AD、A′D′是高线∴∠ADB=A′D′B′=90°∠∴△ABDA′B′D∽△′角平分线角平分线中线中线②②相似三角形的相似三角形的对应角平分线之比,对应角平分线之比,中线之比,中线之比,都等于都等于相似比。相似比。((11)如图)如图ΔABC∽ΔAΔABC∽ΔA//BB//CC//,相似比为,相似比为kk,它,它们的面积比是多少?们的面积比是多少?kDAADACCACBBCBAAB````````2```````2121kkkDACBADBCSSCBAABC①①相似三角形相似三角形面积的比面积的比等于等于相似比的平方相似比的平方..ABCDA/B/C/D/探一探((22)如图,四边)如图,四边ABCDABCD相似于四边形相似于四边形AA//BB//CC//DD//,相似比为,相似比为kk,它们的面积比是多少?,它们的面积比是多少?ABCDA/B/C/D/②②相似多边形相似多边形面积的比面积的比等于等于相似比的平方相似比的平方..((11)相似三角形对应的比等于)相似三角形对应的比等于相似比相似比..相似三角形相似三角形((多边形多边形))的性质的性质::((33)相似)相似面积面积的比等于的比等于相似比的平方相似比的平方..多边形多边形多边形多边形((22)相似)相似周长周长的比等于的比等于相似比相似比..三角形三角形三角形三角形高线高线角平分线角平分线中线中线知识归纳(1)已知ΔABC与ΔA/B/C/的相似比为2:3,则周长比为,对应边上中线之比,面积之比为。(2)已知ΔABCΔA∽/B/C/,且面积之比为9:4,则周长之比为,相似比,对应边上的高线之比。2:34:93:23:23:22:3练一练3.如果两个相似三角形的面积之比为2:7,较大三角形一边上的高为7,则较小三角形对应边上的高为______。14例例11、、如图在如图在ΔABCΔABC和和ΔDEFΔDEF中,中,AB=2DEAB=2DE,,AC=2DFAC=2DF,,∠∠A=∠DA=∠D,,ΔABCΔABC的周长是的周长是2424,,面积是,求面积是,求ΔDEFΔDEF的周长和面积。的周长和面积。ABCDEF512解:在△ABC和△DEF中, AB=2DE,AC=2DF,∴21ACDFABDE又∠D=∠A,∴△DEF∽△ABC,相似比为21∴△DEF的周长为21×24=12面积为53512()212例题讲解EABCD例例22、如图、如图,,在△在△ABCABC中中,D,D是是ABAB的中点,的中点,DEBC∥DEBC∥则则::(1)S(1)S△ADE△ADE:S:S△ABC△ABC==(2)S(2)S△ADE△ADE:S:S梯形梯形DBCEDBCE==1:41:3这是圆桌正上方的灯泡(当成一个点)发出的光线照射桌面形成阴影的示意图,已知桌面的直径为1.2米,桌面距离地面为1米,若灯泡距离地面3米,则地面上阴影部分的面积为多少?FEDCBAL'LF'FBH△ABC中,DEBC∥,EF...