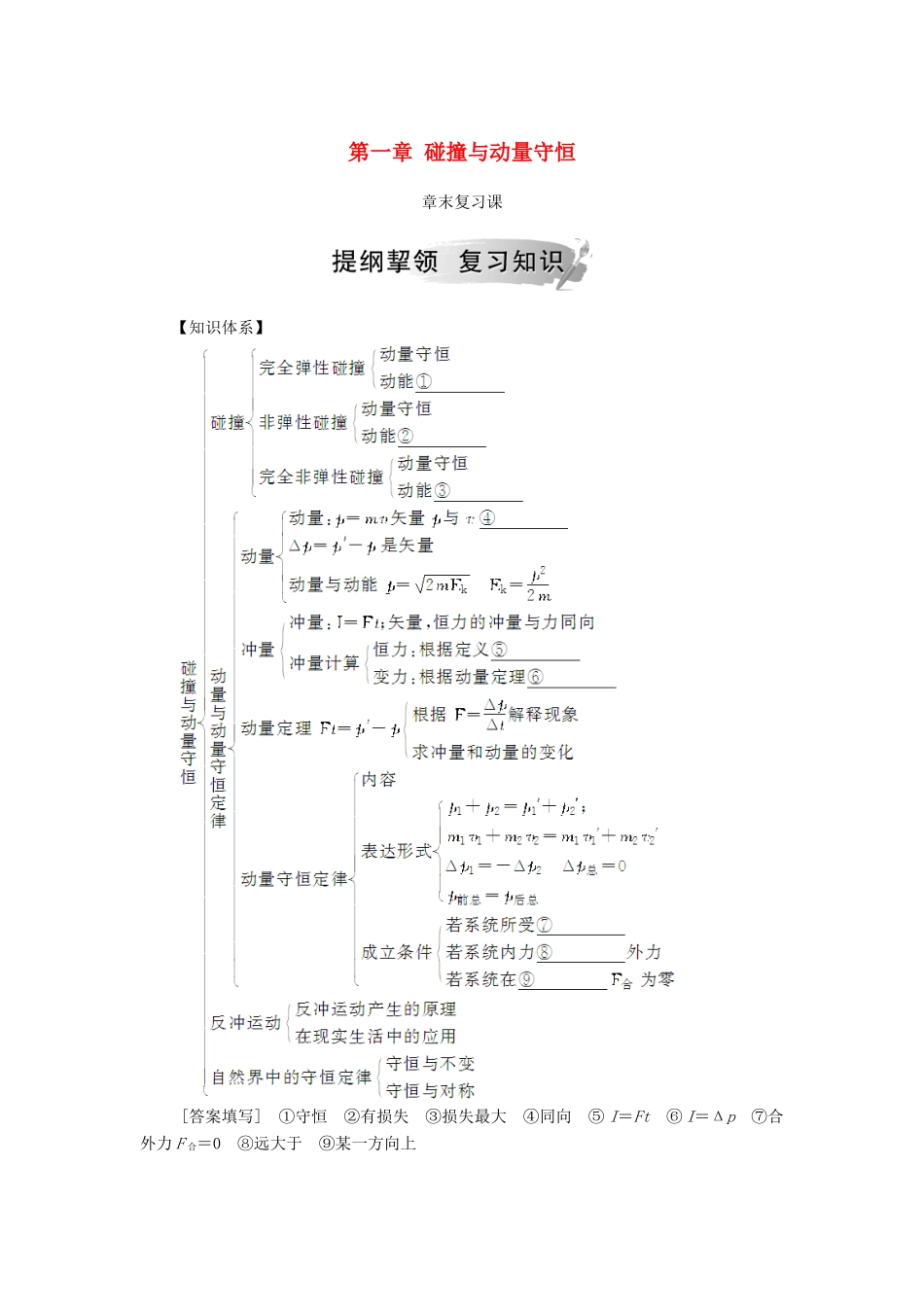
第一章碰撞与动量守恒章末复习课【知识体系】[答案填写]①守恒②有损失③损失最大④同向⑤I=Ft⑥I=Δp⑦合外力F合=0⑧远大于⑨某一方向上主题1动量定理的应用1.动量定理的应用.(1)应用I=Δp求变力的冲量:如果物体受到变力作用,则不能直接用I=F·t求变力的冲量,这时可以求出该力作用下物体动量的变化Δp,即等效代换为变力的冲量I.(2)应用Δp=F·t求恒力作用下的曲线运动中物体动量的变化:曲线运动中物体速度方向时刻在改变,求动量变化Δp=p′-p需要应用矢量运算方法,比较复杂.如果作用力是恒力,可以求恒力的冲量,等效代换动量的变化.(3)用动量定理解释现象:用动量定理解释的现象一般可分为两类:一类是物体的动量变化一定,分析力与作用时间的关系;另一类是作用力一定,分析力作用时间与动量变化间的关系.分析问题时,要把哪个量一定、哪个量变化搞清楚.(4)处理连续流体问题(变质量问题)通常选取流体为研究对象,对流体应用动量定理列式求解.2.应用动量定理解题的步骤.(1)选取研究对象;(2)确定所研究的物理过程及其始、末状态;(3)分析研究对象在所研究的物理过程中的受力情况;(4)规定正方向,根据动量定理列方程式;(5)解方程,统一单位,求解结果.[典例❶]宇宙飞船在太空飞行时,如果遇到微陨石云,会受到较大的阻力.微陨石云是太空中游离的物质微粒比较集中的区域.已知宇宙飞船沿运行方向的横截面积为S,运行速度为v,微陨石云的平均密度为ρ,设宇宙飞船接触到的微陨石最后都附着在飞船上.求宇宙飞船在穿越微陨石云过程中所受阻力F的大小.解析:设在时间t内,微陨石的总质量m=ρSvt,飞船增加的动量Δp=mv=ρSv2t由动量定理可得:Ft=Δp,解得阻力F=ρSv2答案:F=ρSv2针对训练1.一质量为0.5kg的小物块放在水平地面上的A点,距离A点5m的位置B处是一面墙,如图所示.长物块以v0=9m/s的初速度从A点沿AB方向运动,在与墙壁碰撞前瞬间的速度为7m/s,碰后以6m/s的速度反向运动直至静止.g取10m/s2.(1)求物块与地面间的动摩擦因数μ;(2)若碰撞时间为0.05s,求碰撞过程中墙面对物块平均作用力的大小F;(3)求物块在反向运动过程中克服摩擦力所做的功W.解析:(1)由动能定理,有:-μmgs=mv2-mv,可得μ=0.32.(2)由动量定理,有FΔt=mv′-mv,可得F=130N.(3)W=mv′2=9J.答案:(1)μ=0.32(2)F=130N(3)W=9J主题2动量守恒中的临界问题在动量守恒定律的应用中,常常会遇到相互作用的两个物体相距最近、避免相碰和开始反向等临界问题,分析临界问题的关键是寻找临界状态,在与动量相关的临界问题中,临界条件常常表现为两个物体的相对速度关系和相对位移关系,这些特定关系的判断是求解这类问题的切入点.【典例2】质量为M=6kg的木板B静止于光滑水平面上,物块A质量为6kg,停在B的左端.质量为1kg的小球用长为0.8m的轻绳悬挂在固定点O上,将轻绳拉直至水平位置后,由静止释放小球,小球在最低点与A发生碰撞后反弹,反弹所能达到的最大高度为0.2m,物块与小球可视为质点,不计空气阻力.已知A、B间的动摩擦因数μ=0.1,为使A、B达到共同速度前A不滑离木板,木板至少多长?解析:mgL=mv,v1==4m/s,mgh=mv′,v′1==2m/s.球与A碰撞过程中,系统动量守恒mv1=-mv′1+mAvA得vA=1m/s.物块A与木板B相互作用过程中mAvA=(mA+M)v共v共=0.5m/s.μmAgx=mAv-(mA+M)v,得x=0.25m.答案:0.25m针对训练2.如图所示,固定的光滑圆弧面与质量为6kg的小车C的上表面平滑相接,在圆弧面上有一个质量为2kg的滑块A,在小车C的左端有一个质量为2kg的滑块B,滑块A与B均可看作质点.现使滑块A从距小车的上表面高h=1.25m处由静止下滑,与B碰撞后瞬间黏合在一起共同运动,最终没有从小车C上滑出.已知滑块A、B与小车C的动摩擦因数均为μ=0.5,小车C与水平地面的摩擦忽略不计,g取10m/s2.求:(1)滑块A与B碰撞后瞬间的共同速度的大小;(2)小车C上表面的最短长度.解析:(1)设滑块A滑到圆弧末端时的速度大小为v1,由机械能守恒定律有:mAgh=mAv,①代入数据解得v1=5m/s.②设A、B碰后瞬间的共同速度为v2,滑块A与B碰撞瞬间与车C无关,滑块A与B组...