湖南省益阳市高三数学 直线、平面平行的判定与性质复习教案-人教版高三全册数学教案VIP免费

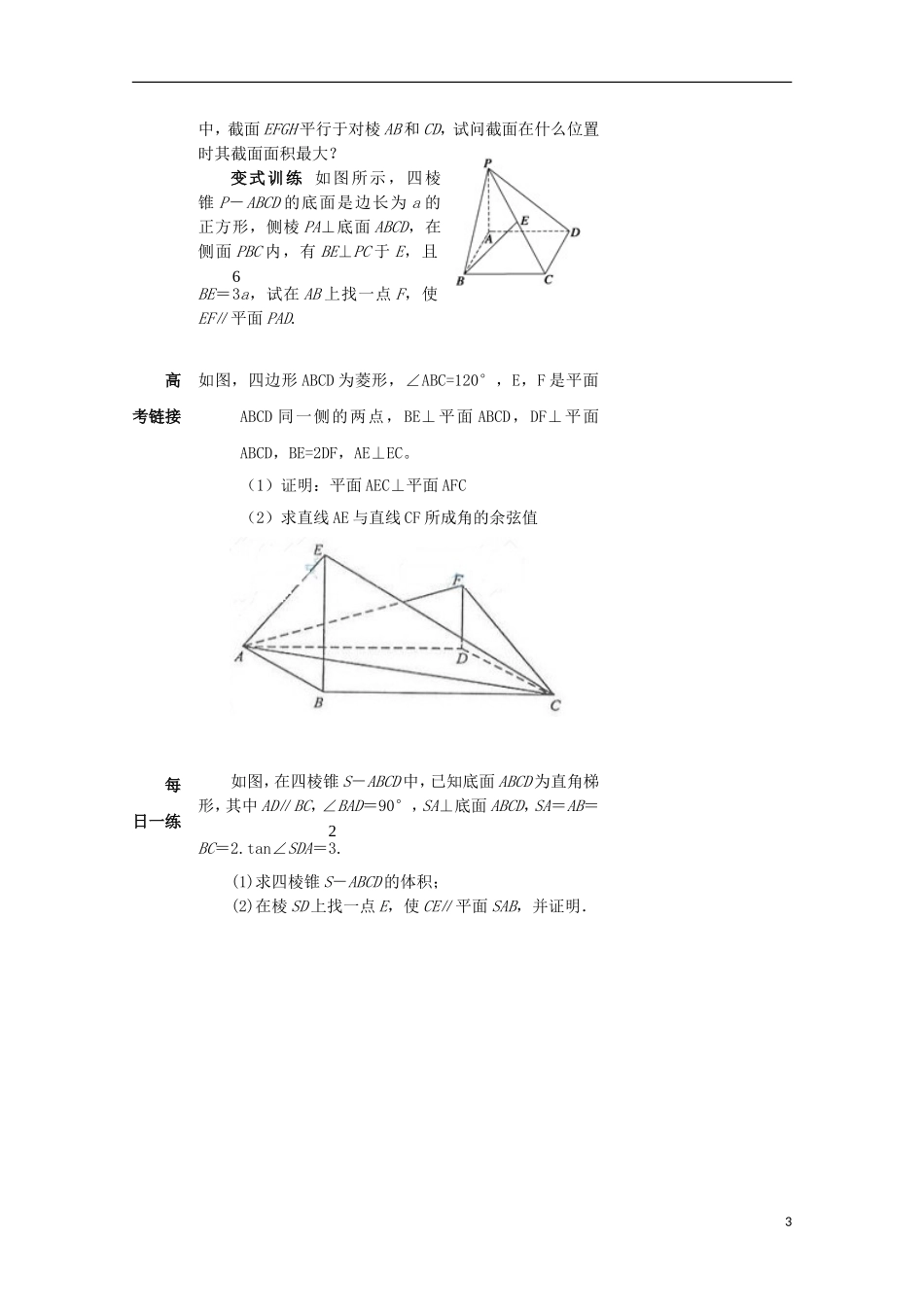
直线、平面平行的判定与性质课题直线、平面平行的判定与性质备注三维目标掌握线线，线面平行的判定和性质，能进行灵活的应用培养学生的空间想象能力和严谨的逻辑思维能力重点掌握线线，线面平行的判定和性质难点能进行线线，线面平行的判定和性质灵活的应用辨析(1)如果一个平面内的两条直线平行于另一个平面，那么这两个平面平行．(×)(2)如果两个平面平行，那么分别在这两个平面内的两条直线平行或异面．(√)(3)若直线a与平面α内无数条直线平行，则a∥α.(×)(4)空间四边形ABCD中，E，F分别是AB，AD的中点，则EF∥平面BCD.(√)(5)若α∥β，直线a∥α，则a∥β.(×)考点自测1．设α，β，γ为三个不同的平面，m，n是两条不同的直线，在命题“α∩β＝m，n⊂γ，且________，则m∥n”中的横线处填入下列三组条件中的一组，使该命题为真命题．①α∥γ，n⊂β；②m∥γ，n∥β；③n∥β，m⊂γ.可以填入的条件有()A．①或②B．②或③C．①或③D．①或②或③2．下列命题中，错误的是()A．平面内一个三角形各边所在的直线都与另一个平面平行，则这两个平面平行B．平行于同一个平面的两个平面平行C．若两个平面平行，则位于这两个平面内的直线也互相平行D．若两个平面平行，则其中一个平面内的直线平行于另一个平面3．空间中，下列命题正确的是()A．若a∥α，b∥a，则b∥α1B．若a∥α，b∥α，a⊂β，b⊂β，则β∥αC．若α∥β，b∥α，则b∥βD．若α∥β，a⊂α，则a∥β4．如图，正方体ABCD－A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长度等知识梳理1．直线与平面平行的判定与性质2.面面平行的判定与性质例题选讲题型一直线与平面平行的判定与性质例1如图，四棱锥P－ABCD中，AD∥BC，AB＝BC＝12AD，E，F，H分别为线段AD，PC，CD的中点，AC与BE交于O点，G是线段OF上一点．(1)求证：AP∥平面BEF；(2)求证：GH∥平面PAD.变式训练如图，在四棱锥P—ABCD中，PD⊥平面ABCD，AB∥DC，AB⊥AD，BC＝5，DC＝3，AD＝4，∠PAD＝60°.(1)若M为PA的中点，求证：DM∥平面PBC；(2)求三棱锥D—PBC的体积．题型二平面与平面平行的判定与性质例2如图，四棱柱ABCD－A1B1C1D1的底面ABCD是正方形，O为底面中心，A1O⊥平面ABCD，AB＝AA1＝.(1)证明：平面A1BD∥平面CD1B1；(2)求三棱柱ABD－A1B1D1的体积．变式训练如图，在正方体ABCD－A1B1C1D1中，S是B1D1的中点，E、F、G分别是BC、DC、SC的中点，求证：(1)直线EG∥平面BDD1B1；(2)平面EFG∥平面BDD1B1.例3如图所示，在四面体ABCD2中，截面EFGH平行于对棱AB和CD，试问截面在什么位置时其截面面积最大？变式训练如图所示，四棱锥P－ABCD的底面是边长为a的正方形，侧棱PA⊥底面ABCD，在侧面PBC内，有BE⊥PC于E，且BE＝63a，试在AB上找一点F，使EF∥平面PAD.高考链接如图，四边形ABCD为菱形，∠ABC=120°，E，F是平面ABCD同一侧的两点，BE⊥平面ABCD，DF⊥平面ABCD，BE=2DF，AE⊥EC。（1）证明：平面AEC⊥平面AFC（2）求直线AE与直线CF所成角的余弦值每日一练如图，在四棱锥S－ABCD中，已知底面ABCD为直角梯形，其中AD∥BC，∠BAD＝90°，SA⊥底面ABCD，SA＝AB＝BC＝2.tan∠SDA＝23.(1)求四棱锥S－ABCD的体积；(2)在棱SD上找一点E，使CE∥平面SAB，并证明．3后记4