112余弦定理1VIP免费

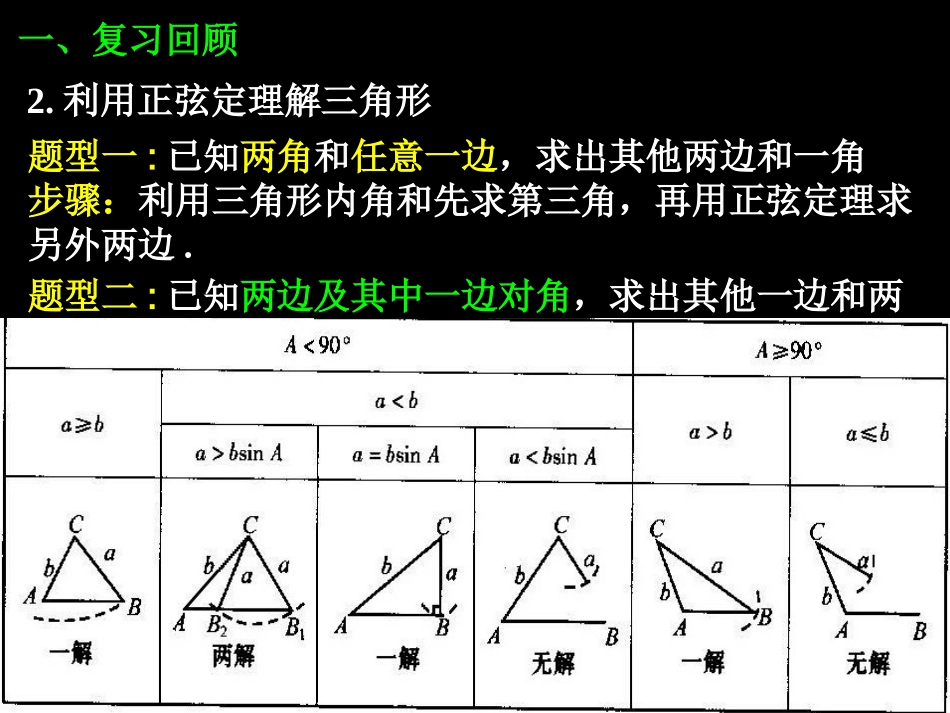
高中新课程数学必修⑤一、复习回顾1.正弦定理及其推论：sinsinsinabcABC=2R(R为△ABC外接圆半径）222sin,sin,sinaRAbRBcRC222sin,sin,sinabcABCRRRsin:sin:sin::ABCabcBCAabc思考：在△ABC中,已知AB=2,BC=5,△ABC的面积为4，∠ABC=θ，则sinθ=.45111sinsinsin222ABCSbcAcaBabC三角形面积公式：练习：在△ABC中，，求此三角形的面积．333315,,acC3332或2.利用正弦定理解三角形题型一:已知两角和任意一边，求出其他两边和一角步骤：利用三角形内角和先求第三角，再用正弦定理求另外两边.题型二:已知两边及其中一边对角，求出其他一边和两角一、复习回顾若已知a、b、A的值，则解该三角形的步骤如下：（1）先利用求出sinB，从而求出角B；（2）利用A、B求出角C=180o-(A+B)；（3）再利用求出边c.sinsinabABsinsinacAC注意：求角B时应注意检验！ABCcab依条件可知，2222cos即cababC同理可得2222222cos,2cosabcbcAbacacB二、新课讲解问题：在△ABC中，a=8，b=3，C=60o，求c.如图，在△ABC中，BC=a，AC=b，边BC与AC的夹角为C，试求AB边的长c.题型三:已知三角形的两条边及其夹角,求出另一边。三角形任何一边的平方等于其他两边的平方和减去这两边与它们夹角的余弦的积的两倍，即余弦定理：2222cosbacacB2222cosabcbcA2222coscababC注：利用余弦定理，可以从已知的两边及其夹角求出三角形的第三条边二、新课讲解例1：在△ABC中，已知b=60cm，c=34cm，A=41o，解该三角形（角度精确到1°，边长精确到1cm）.解：∵a²=b²+c²-2bccosA=60²+34²-2×60×34×cos41o≈1676.82∴a≈41(cm)故由正弦定理可得sin34sin41340.656sin0.5440.4141cACa°´=»»»∵c