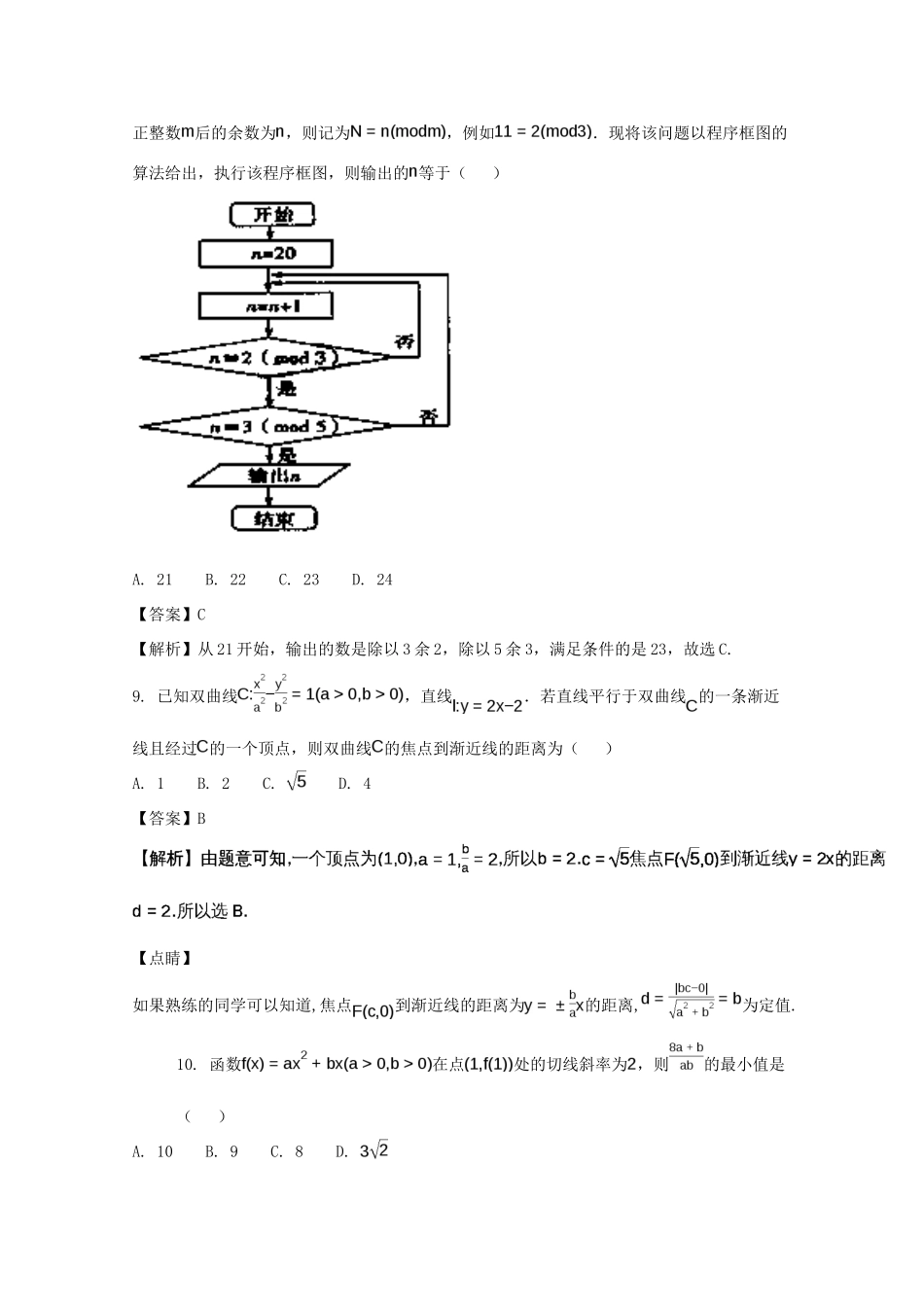
衡阳市2017年高考适应考试试题文科数学一、选择题(本大题共12小题,每小题5分,共60分)1.设全集,集合,则的子集的个数是()A.1B.2C.3D.4【答案】D【解析】全集,集合,,共2个元素,所以的子集的个数是22=4,故选D.2.命题:,的否定是()A.,B.,C.,D.,【答案】A【解析】全称命题:,的否定是,3.在复平面内,复数对应的点坐标为()A.(-1,3)B.(3,1)C.(1,3)D.【答案】C【解析】,对应的点坐标为(1,3),故选C.4.在区间上随机选取一个数,则的概率为()A.B.C.D.【答案】B【解析】因为,所以由几何概型的计算公式可得,故选B.5.公比为2的等比数列的各项都是正数,且,则()A.1B.2C.4D.8【答案】A【解析】试题分析:在等比数列中,由知,,故选A.考点:等比数列的性质.6.已知向量,均为单位向量,若它们的夹角为60°,则等于()A.B.C.D.4【答案】C【解析】,所以.故选C.点睛:平面向量的数量积计算问题,往往有两种形式,一是利用数量积的定义式,二是利用数量积的坐标运算公式,涉及几何图形的问题,先建立适当的平面直角坐标系,可起到化繁为简的妙用.利用向量夹角公式、模公式及向量垂直的充要条件,可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决.列出方程组求解未知数.7.函数的部分图象如图所示,若将图象上所有的点的横坐标缩短为原来的倍(纵坐标不变),得到函数的图象,则的解析式为()A.B.C.D.【答案】D【解析】由图像得,,所以,横坐标缩短为原来一半,得到.8.中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数除以正整数后的余数为,则记为,例如.现将该问题以程序框图的算法给出,执行该程序框图,则输出的等于()A.21B.22C.23D.24【答案】C【解析】从21开始,输出的数是除以3余2,除以5余3,满足条件的是23,故选C.9.已知双曲线,直线.若直线平行于双曲线的一条渐近线且经过的一个顶点,则双曲线的焦点到渐近线的距离为()A.1B.2C.D.4【答案】B【点睛】如果熟练的同学可以知道,焦点到渐近线的距离为的距离,为定值.10.函数在点处的切线斜率为,则的最小值是()A.10B.9C.8D.【答案】B【解析】试题分析:求出原函数的导函数,由得,把变形为后整体乘以1,展开后利用基本不等式求最小值.当且仅当时“=”成立.所以的最小值是9,故选B考点:导数的运算;基本不等式11.某三棱锥的三视图如图所示,则该三棱锥最长的棱长为()A.1B.C.3D.2【答案】C【解析】三视图还原图形三棱锥,如下图:,所以最长边为,选C.12.已知函数与函数的图象上恰有两对关于轴对称的点,则实数的取值范围是()A.B.C.D.【答案】A【解析】由题意可将问题转化为方程在上有两个不等的实数根,即方程有两个不等的实数根,令,则,当时,,函数单调递增;当时,,函数单调递减。所以函数;又,,而,所以结合图像可知当时,函数与直线的图像有两个不同的交点,应选答案A。点睛:解答本题的关键是运用转化与化归思想将问题化为有两个不等的实数根,然后运用导数知识探求得函数的图像的变化情况,借助函数的图像求出参数的取值范围,进而获得答案。二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.)13.某中学高中一年级、二年级、三年级的学生人数比为,现要用分层抽样的方法抽取一个容量为的样本,则所抽取的二年级学生的人数是_________;【答案】80【解析】试题分析: 高中一年级、二年级、三年级的学生人数比为,∴抽取一个容量为240的样本,则所抽取的二年级学生的人数,故答案为:80.考点:分层抽样方法.14.若实数满足则的最小值为__________;【答案】-6【解析】在同一坐标系中,分别作出直线x+y−2=0,x=4,y=5,标出不等式组表示的平面区域,如图所示。由z=y−x,得y=x+z,此关系式可表示斜率为1,纵截距为z的直线,当直线y=x+z经过区域内的点A时,z最小,此时,由,得A(4,−2),从而zmin=y−x=−2−4=−6.点睛:线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一、准确无误地作出可行域;二、画标准函数...