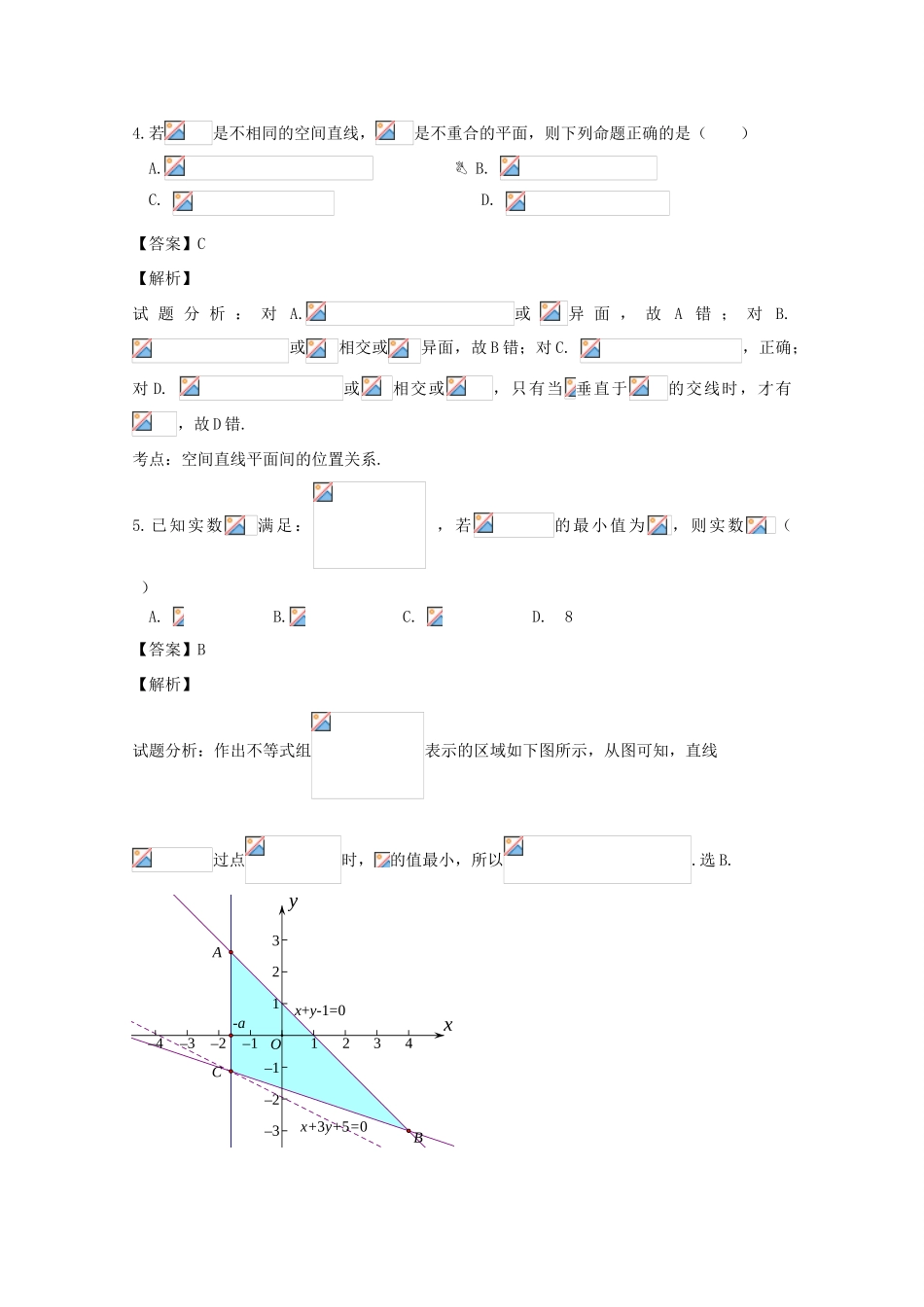
浙江省衢州市2015届高三数学4月教学质量检测试题理(含解析)第Ⅰ卷(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,,则下列结论正确的是()A.B.C.D.【答案】C【解析】试题分析:,所以,选C.考点:集合的基本运算.2.下列函数中,在其定义域上既是奇函数又是增函数的是()A.B.C.D.【答案】B考点:函数的奇偶性及单调性.3.已知直线,,则“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A【解析】试题分析:当时,,所以.故为充分条件.当时,,所以不是必要条件.选A.考点:1、充要条件;2、平面内两直线的垂直关系.4.若是不相同的空间直线,是不重合的平面,则下列命题正确的是()A.B.C.D.【答案】C【解析】试题分析:对A.或异面,故A错;对B.或相交或异面,故B错;对C.,正确;对D.或相交或,只有当垂直于的交线时,才有,故D错.考点:空间直线平面间的位置关系.5.已知实数满足:,若的最小值为,则实数()A.B.C.D.8【答案】B【解析】试题分析:作出不等式组表示的区域如下图所示,从图可知,直线过点时,的值最小,所以.选B.xyx+3y+5=0x+y-1=0–1–2–3–4–51234–1–2–3123ABCO-a考点:线性规划.6.为了得到函数的图像,可以将函数的图像()A.向右平移B.向右平移C.向左平移D.向左平移【解析】D试题分析:,所以将的图象向左平移可得的图象.考点:三角函数图象的变换.7.设点是曲线上的动点,且满足,则的取值范围为()A.B.C.D.【答案】AxyCBF2F1OB1ADxyCBF2F1OB1AD考点:1、曲线与方程;2、不等式.8.在等腰梯形中,其中,以为焦点且过点的双曲线的离心率为,以为焦点且过点的椭圆的离心率为,若对任意不等式恒成立,则的最大值为()A.B.C.2D.【答案】B【解析】试题分析:设双曲线的实半轴为,则.设椭圆的长半轴为,则.所以.令,则,在上,都为增函数,又,所以在上,,从而,所以在上单调递减.又在上单调递减,所以在上单调递减,故,即.若对任意不等式恒成立,则.选B.xyx1CDAB(1,0)Oxyx11BADCO考点:1、圆锥曲线;2、函数的应用.第Ⅱ卷(共100分)二、填空题(每题5分,满分25分,将答案填在答题纸上)9.已知双曲线:,则它的焦距为___;渐近线方程为___;焦点到渐近线的距离为___.【答案】.【解析】试题分析:所以焦距为,渐近线方程为,焦点到准线的距离即为.考点:双曲线.10.已知等差数列的前项和为,,,则__,__.【答案】【解析】试题分析:由题设得:,解之得:,.考点:等差数列.11.三棱锥中,平面,为侧棱上一点,它的正视图和侧视图(如下图所示),则与平面所成角的大小为___;三棱锥的体积为___.【答案】【解析】试题分析:由题设及正视图可知,又由平面得,所以平面,即与平面所成角为.三棱锥的体积.考点:1、三视图;2、三棱锥的体积.12.在中,若,则其形状为___,__.(①锐角三角形②钝角三角形③直角三角形,在横线上填上序号);【答案】③,【解析】试题分析:由知,,所以是直角三角形,,利用数量积的几何意义得.考点:平面向量.13.已知满足方程,当时,则的最小值为__.【答案】8【解析】试题分析:.易知表示抛物线上的点与点的连线的斜率,从图可知,所以.考点:重要不等式.14.过抛物线的焦点作一条倾斜角为锐角,长度不超过的弦,且弦所在的直线与圆有公共点,则角的最大值与最小值之和是___.【答案】【解析】试题分析:抛物线的焦点为,则过焦点的直线方程为,代入得,弦长为.据题意得,所以.将变形得,由得,综合得,所以角的最大值与最小值之和.考点:直线与圆锥曲线.15.已知函数,若关于的方程有个不同的实数根,且所有实数根之和为,则实数的取值范围为___.【答案】【解析】考点:函数与方程.三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.(本题满分15分)已知函数.(Ⅰ)求函数的单调增区间;(Ⅱ)在中,内角所对边分别为,,若对任意的不等式恒成立,求面积的最大值.【答案】(Ⅰ);(Ⅱ).【解析】试题分析:(Ⅰ)将函数降次化一得,根据正弦函数的单调性可得函...