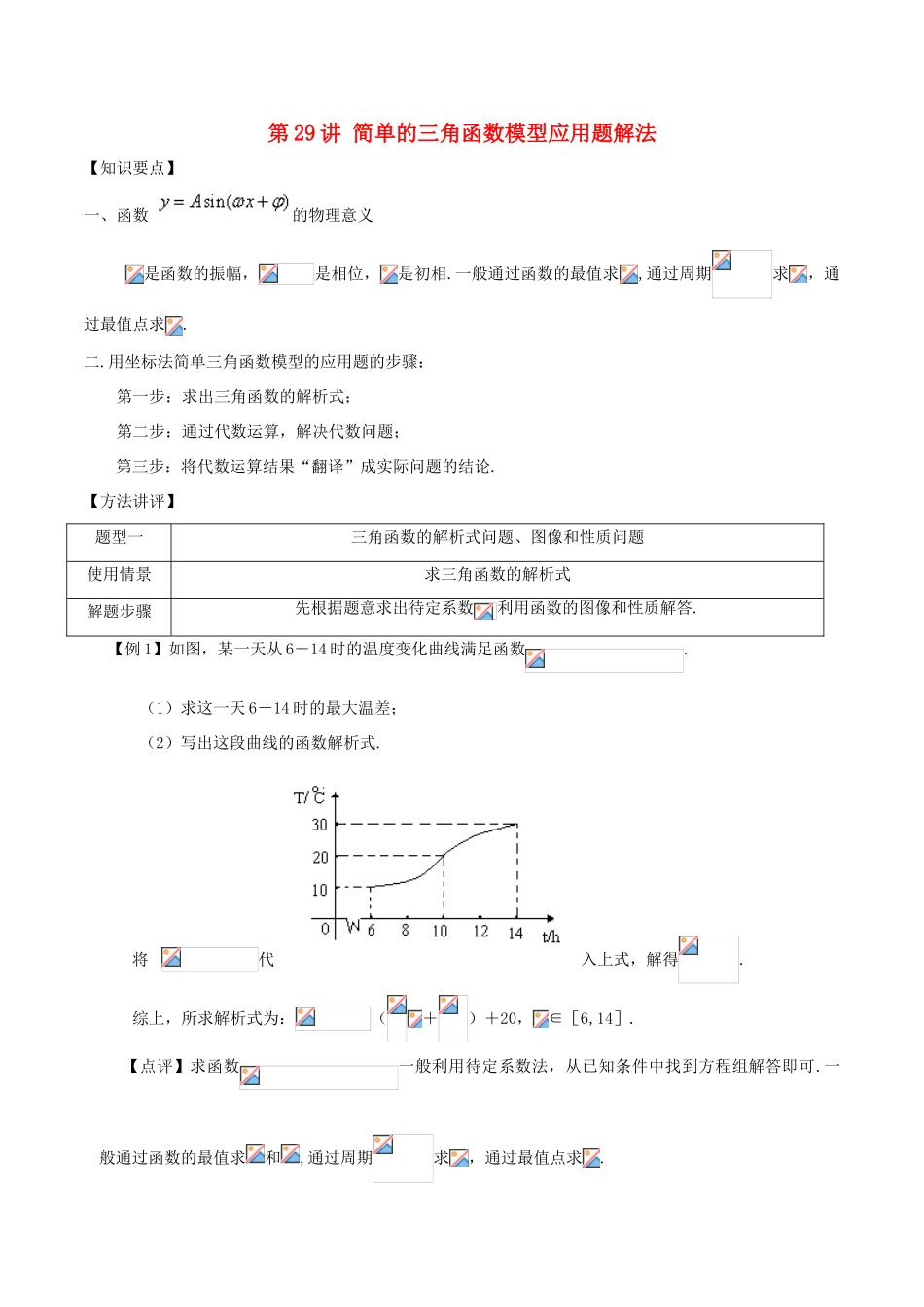
第29讲简单的三角函数模型应用题解法【知识要点】一、函数的物理意义是函数的振幅,是相位,是初相.一般通过函数的最值求,通过周期求,通过最值点求.二.用坐标法简单三角函数模型的应用题的步骤:第一步:求出三角函数的解析式;第二步:通过代数运算,解决代数问题;第三步:将代数运算结果“翻译”成实际问题的结论.【方法讲评】题型一三角函数的解析式问题、图像和性质问题使用情景求三角函数的解析式解题步骤先根据题意求出待定系数利用函数的图像和性质解答.【例1】如图,某一天从6―14时的温度变化曲线满足函数.(1)求这一天6-14时的最大温差;(2)写出这段曲线的函数解析式.将代入上式,解得.综上,所求解析式为:(+)+20,∈[6,14].【点评】求函数一般利用待定系数法,从已知条件中找到方程组解答即可.一般通过函数的最值求和,通过周期求,通过最值点求.【例2】某地有三家工厂,分别位于矩形的顶点,及的中点处,已知,,为了处理三家工厂的污水,现要在矩形的区域上(含边界),且,与等距离的一点处建造一个污水处理厂,并铺设排污管道,,,设排污管道的总长为.(Ⅰ)按下列要求写出函数关系式:①设,将表示成的函数关系式;②设,将表示成的函数关系式.(Ⅱ)请你选用(Ⅰ)中的一个函数关系式,确定污水处理厂的位置,使三条排污管道总长度最短.(Ⅱ)选择函数模型①,【点评】(1)本题主要考查根据实际意义建立函数模型、三角函数性质和解决最值问题的基本知识,考查了数形结合思想和分析问题、转化求解的能力.(2)对于较复杂的三角函数的最值,一般利用导数来研究函数的单调性从而得到函数的最值.(3)一般以平面几何为背景的应用题,多以角为自变量建立三角函数模型,比以边为自变量建立函数模型简单.【反馈检测1】如图所示,某园林单位准备绿化一块直径为的半圆形空地,外的地方种草,的内接正方形为一水池,其余地方种花.若,,设的面积为,正方形的面积为.(1)(2)当固定,变化时,求取得最小值时的值.题型二潮汐进出港和海滨冲浪问题使用情景潮汐进出港和海滨冲浪问题ABCPQRSθ解题步骤一般先求出三角函数的解析式,再解三角函数不等式.【例2】已知某海滨浴场的海浪高度(单位:米)与时间(单位:时)的函数关系记作,下表是某日各时的浪高数据:经长期观测,的曲线可近似地看成是函数.(1)根据以上数据,求函数的最小正周期,振幅及函数表达式;(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8∶00时至晚上20∶00时之间,有多少时间可供冲浪者进行运动? ,故可令①中分别为,得或或.∴在规定时间上午至晚上之间,有6个小时时间可供冲浪者运动,即上午至下午.【点评】(1)首先要利用三角函数的图像和性质求出三角函数的表达式,是函数的振幅,(时)03691215182124(米)1.51.00.51.01.51.00.51.01.5是相位,是初相.一般通过函数的最值求,通过周期求,通过最值点求.(2)解简单的三角函数不等式主要是利用三角函数的图像和数形结合的思想解答.三角不等式的解集中一般含有“”,最后给赋值和实际范围求交集.【反馈检测2】海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天从0时至24时的时间(单位:时)与水深(单位:米)的关系表:(1)请选用一个函数来近似描述这个港口的水深与时间的函数关系;(2)一条货轮的吃水深度(船体最低点与水面的距离)为12米,安全条例规定船体最低点与洋底间隙至少要有1.5米,请问该船何时能进出港口?在港口最多能停留多长时间?高中数学常见题型解法归纳及反馈检测第29讲:简单的三角函数模型应用题解法参考答案【反馈检测1答案】(1);(2)【反馈训练2答案】(1);(2)货船在1点至5点可以进出港;或13点至17点可以进出港.每次可以在港口最多能停留4小时.【反馈检测2详细解析】(1)以时间为横坐标,水深为纵坐标,考虑用函数刻画水深与时间之间的对应关系.从数据可以得出:由,得.所以这个港口的水深与时间的关系可...