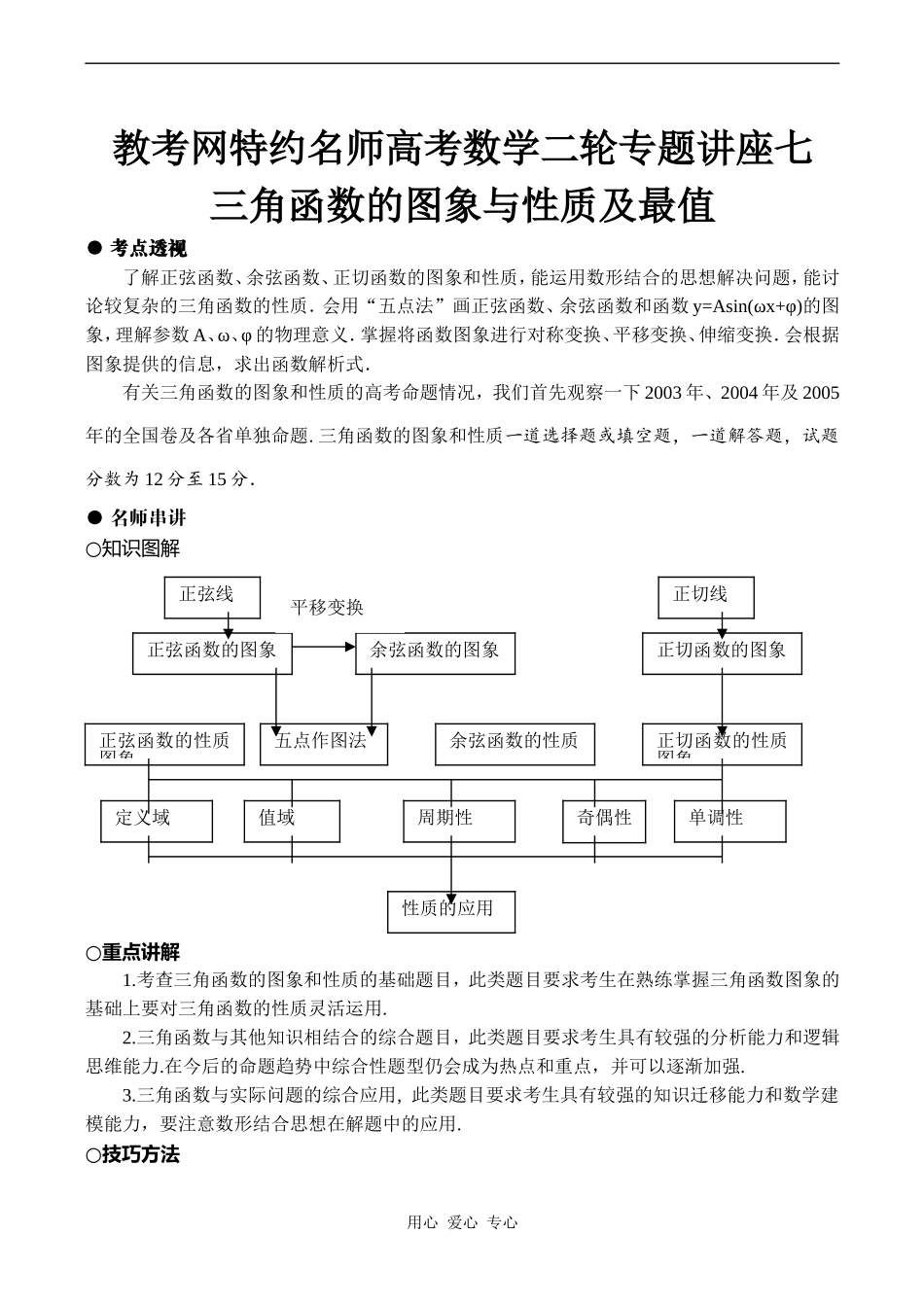
教考网特约名师高考数学二轮专题讲座七三角函数的图象与性质及最值●考点透视了解正弦函数、余弦函数、正切函数的图象和性质,能运用数形结合的思想解决问题,能讨论较复杂的三角函数的性质.会用“五点法”画正弦函数、余弦函数和函数y=Asin(ωx+φ)的图象,理解参数A、ω、φ的物理意义.掌握将函数图象进行对称变换、平移变换、伸缩变换.会根据图象提供的信息,求出函数解析式.有关三角函数的图象和性质的高考命题情况,我们首先观察一下2003年、2004年及2005年的全国卷及各省单独命题.三角函数的图象和性质一道选择题或填空题,一道解答题,试题分数为12分至15分.●名师串讲○知识图解○重点讲解1.考查三角函数的图象和性质的基础题目,此类题目要求考生在熟练掌握三角函数图象的基础上要对三角函数的性质灵活运用.2.三角函数与其他知识相结合的综合题目,此类题目要求考生具有较强的分析能力和逻辑思维能力.在今后的命题趋势中综合性题型仍会成为热点和重点,并可以逐渐加强.3.三角函数与实际问题的综合应用,此类题目要求考生具有较强的知识迁移能力和数学建模能力,要注意数形结合思想在解题中的应用.○技巧方法用心爱心专心正弦线正弦函数的图象余弦函数的图象正弦函数的性质图象余弦函数的性质五点作图法正切函数的图象正切函数的性质图象正切线定义域值域周期性奇偶性单调性性质的应用平移变换讨论较复杂的三角函数的性质,往往需要将原函数式进行化简,其目标为转化成同一个角的同名三角函数问题.讨论三角函数的单调性,解三角不等式,要注意数形结合思想的运用.注意函数性质在解题中的运用:若一个函数为周期函数,则讨论其有关问题,可先研究在一个周期内的情形,然后再进行推广;若要比较两个角的三角函数值的大小,可考虑运用三角函数的单调性加以解决.已知三角函数y=Asin(ωx+φ)的图象,欲求其解析式,必须搞清A、ω、φ和图象的哪些因素有关;y=sinωx和y=sin(ωx+φ)两图象间平移变换的方向和平移的单位数量极易搞错,解题时要倍加小心.●考题解析【例1】(2004年湖北卷)设是某港口水的深度y(米)关于时间t(时)的函数,其中.下表是该港口某一天从0时至24时记录的时间t与水深y的关系:t03691215182124y1215.112.19.111.914.911.98.912.1经长期观察,函数的图象可以近似地看成函数的图象.下面的函数中,最能近似表示表中数据间对应关系的函数是(A)A.B.C.D.【思路串讲】“会用三角函数解决一些简单实际问题,体会三角函数是描述周期变化现象的重要函数模型”,是新课程标准中明确提出的要求,并且在新课程标准中提出了如下案例:“海水受日月的引力,在一定的时候发生涨落的现象叫潮,一般地早潮叫潮,晚潮叫汐.在通常的情況下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:时刻水深(米)时刻水深(米)时刻水深(米)0:005.09:002.518:005.03:007.512:005.021:002.56:005.015:007.524:005.0(1)选用一个三角函数来近似描述这个港口的水深与时间的函数关系.给出整点时的水深的近似数值.(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离).该船何时能进入港口?在港口能呆多久?(3)若某船的吃水深度为4米,安全间隙为1.5米,该船在2∶00开始卸货,吃水深度以每小时0.3米的速度减少,那么该船在什么时间必须停止卸货,将船驶向较深的水域?”考题与上述问题是何等的相似.高考从新课程标准与旧知识的衔接处切入问题,引出考题,用心爱心专心这是一个命题导向,这很值得注意,务必引起学生的高度重视.此类问题的求解一般是先找出周期,定出A与是的值,最后确定的值.【标准答案】A【例2】(2000年广东卷)已知函数(Ⅰ)当函数取得最大值时,求自变量的集合;(Ⅱ)该函数的图象可由的图象经过怎样的平移和伸缩变换得到?【思路串讲】本题主要考查三角函数的图象和性质、利用三角公式进行恒等变形的技能以及运算能力.解题突破口:利用三角公式进行恒等变形化简为解决此类问题【标准答案】(1).…………3分取得最大值必...