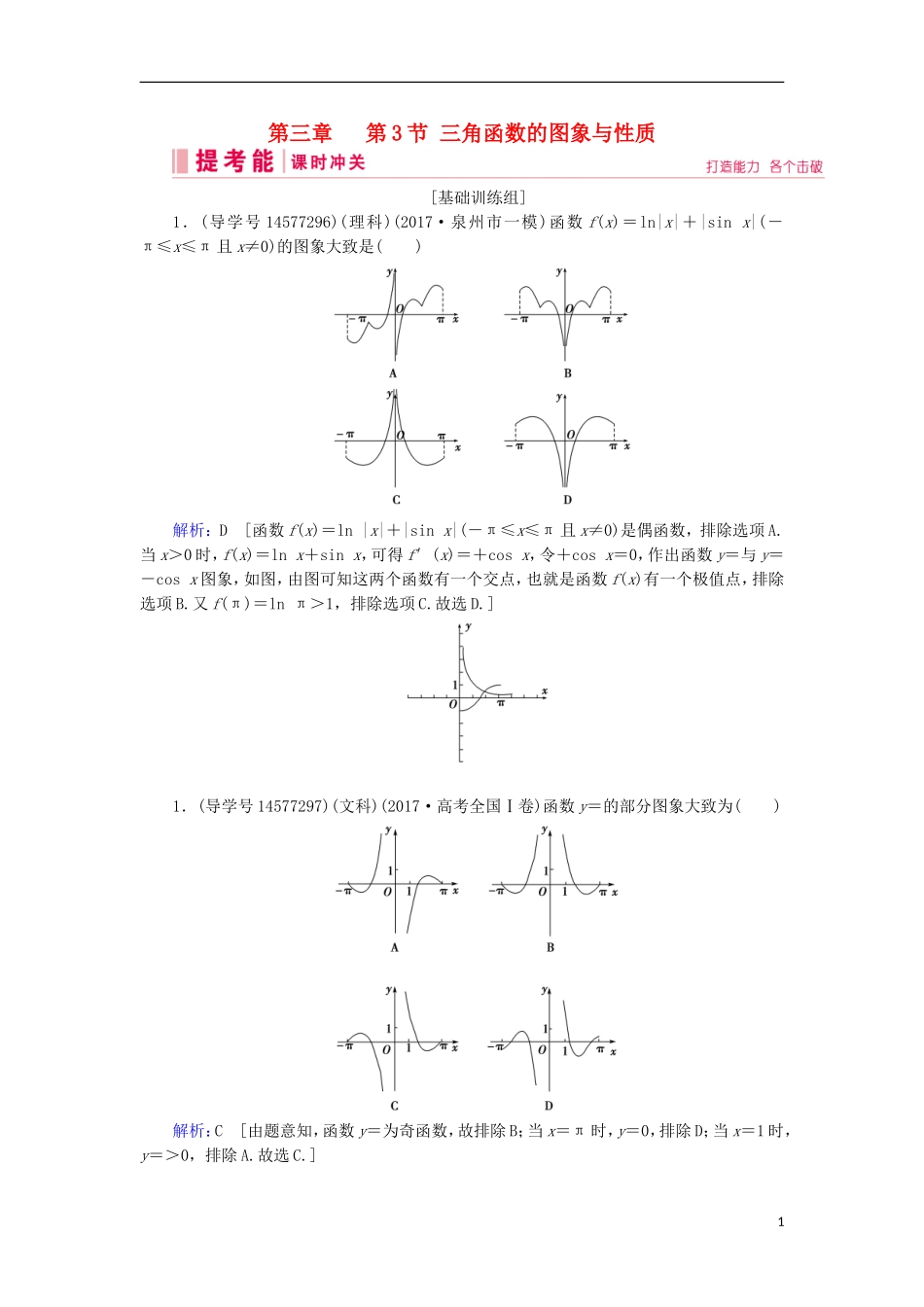
第三章第3节三角函数的图象与性质[基础训练组]1.(导学号14577296)(理科)(2017·泉州市一模)函数f(x)=ln|x|+|sinx|(-π≤x≤π且x≠0)的图象大致是()解析:D[函数f(x)=ln|x|+|sinx|(-π≤x≤π且x≠0)是偶函数,排除选项A.当x>0时,f(x)=lnx+sinx,可得f′(x)=+cosx,令+cosx=0,作出函数y=与y=-cosx图象,如图,由图可知这两个函数有一个交点,也就是函数f(x)有一个极值点,排除选项B.又f(π)=lnπ>1,排除选项C.故选D.]1.(导学号14577297)(文科)(2017·高考全国Ⅰ卷)函数y=的部分图象大致为()解析:C[由题意知,函数y=为奇函数,故排除B;当x=π时,y=0,排除D;当x=1时,y=>0,排除A.故选C.]12.(导学号14577298)(2018·广州市模拟)已知sinφ=,且φ∈,函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于,则f的值为()A.-B.-C.D.解析:B[根据函数f(x)=sin(ωx+φ)(ω>0)的图象的相邻两条对称轴之间的距离等于,可得==,∴ω=2.由sinφ=,且φ∈,可得cosφ=-,∴f=sin=cosφ=-,故选B.]3.(导学号14577299)(2018·邵阳市三模)已知函数f(x)=sin(ω>0)下的最小正周期为π,则函数的图象()A.关于直线x=对称B.关于点对称C.关于直线x=-对称D.关于点对称解析:A[ =π,解得ω=1,∴f(x)=sin,由2x+=kπ+可得x=+,k∈Z,结合选项可知当k=2时,函数一条对称轴为x=,故选A.]4.(导学号14577300)(2018·济宁市三模)若函数f(x)=sin(2x+φ)(|φ|<)的图象关于直线x=对称,且当x1,x2∈,x1≠x2时,f(x1)=f(x2),则f(x1+x2)等于()A.B.C.D.解析:C[ sin=±1,∴φ=kπ+,k∈Z.又 |φ|<,∴φ=,∴f(x)=sin.当x∈,2x+∈,区间内有唯一对称轴x=-. x1,x2∈,x1≠x2时,f(x1)=f(x2),∴x1,x2关于x=-对称,即x1+x2=-π,∴f(x1+x2)=.故选C.]5.(导学号14577301)(2018·莆田市一模)已知函数f(x)=sincos(x∈R),则下列结论错误的是()A.函数f(x)的最小正周期为πB.函数f(x)的图象关于直线x=-对称C.函数f(x)的图象关于点对称D.函数f(x)在区间上是增函数解析:C[f(x)=sincos=sin,由周期公式可得:T==π,故A正确;由2x-=kπ+,得x=+,k=-1时,x=-,故B正确;由2x-=kπ,得x=+,k=-1时,x=-,故,故C错误;由2kπ-≤2x-≤2kπ+,可解得函数的单调递增区间为,k∈Z,故明显D正确;故选C.]26.(导学号14577302)不等式+2cosx≥0的解集是________.解析:由+2cosx≥0,得cosx≥-,由余弦函数的图象,得在一个周期[-π,π]上,不等式cosx≥-的解集为,故原不等式的解集为.答案:7.(导学号14577303)(2018·淮北市一模)函数f(x)=2sinx+2cosx-sin2x+1,x∈的值域是_______________.解析:令t=sinx+cosx,则t2=1+2sinxcosx,即sin2x=t2-1,所以y=f(t)=2t-(t2-1)+1=-t2+2t+2=-(t-1)2+3.又t=sinx+cosx=sin,且x∈,∴x+∈,∴sin∈,∴-≤t≤;∴当t=1时,f(t)取得最大值3;t=-时,f(t)取得最小值-,∴函数y=f(x)的值域为.答案:8.(导学号14577304)函数y=sin(ωx+φ)(ω>0,0<φ<π)的最小正周期为π,且函数图象关于点对称,则函数的解析式为________.解析:由题意知最小正周期T=π=,∴ω=2,2×+φ=kπ,k∈Z,∴φ=kπ+,又0<φ<π,∴φ=,∴y=sin.答案:y=sin9.(导学号14577305)(2018·乐山市一诊)已知函数f(x)=cos2-sin2x.(1)求f的值;(2)若对于任意的x∈,都有f(x)≤c,求实数c的取值范围.解:(1) 函数f(x)=cos2-sin2x,∴f=cos2-sin2=cos=.(2) f(x)=-(1-cos2x)===sin.因为x∈,所以2x+∈,所以当2x+=,即x=时,f(x)取得最大值.所以∀x∈,f(x)≤c等价于≤c.故当∀x∈,f(x)≤c时,c的取值范围是.10.(导学号14577306)已知函数f(x)=cosx·(2sinx-cosx)+asin2x的一个零点是.3(1)求函数f(x)的最小正周期;(2)令x∈,求此时f(x)的最大值和最小值.解:(1)f(x)=cosx(2sinx-cosx)+asin2x=2sinxcosx-cos2x+asin2x,=sin2x-cos2x+asin2x, 一个零点是,∴sin-cos2+...