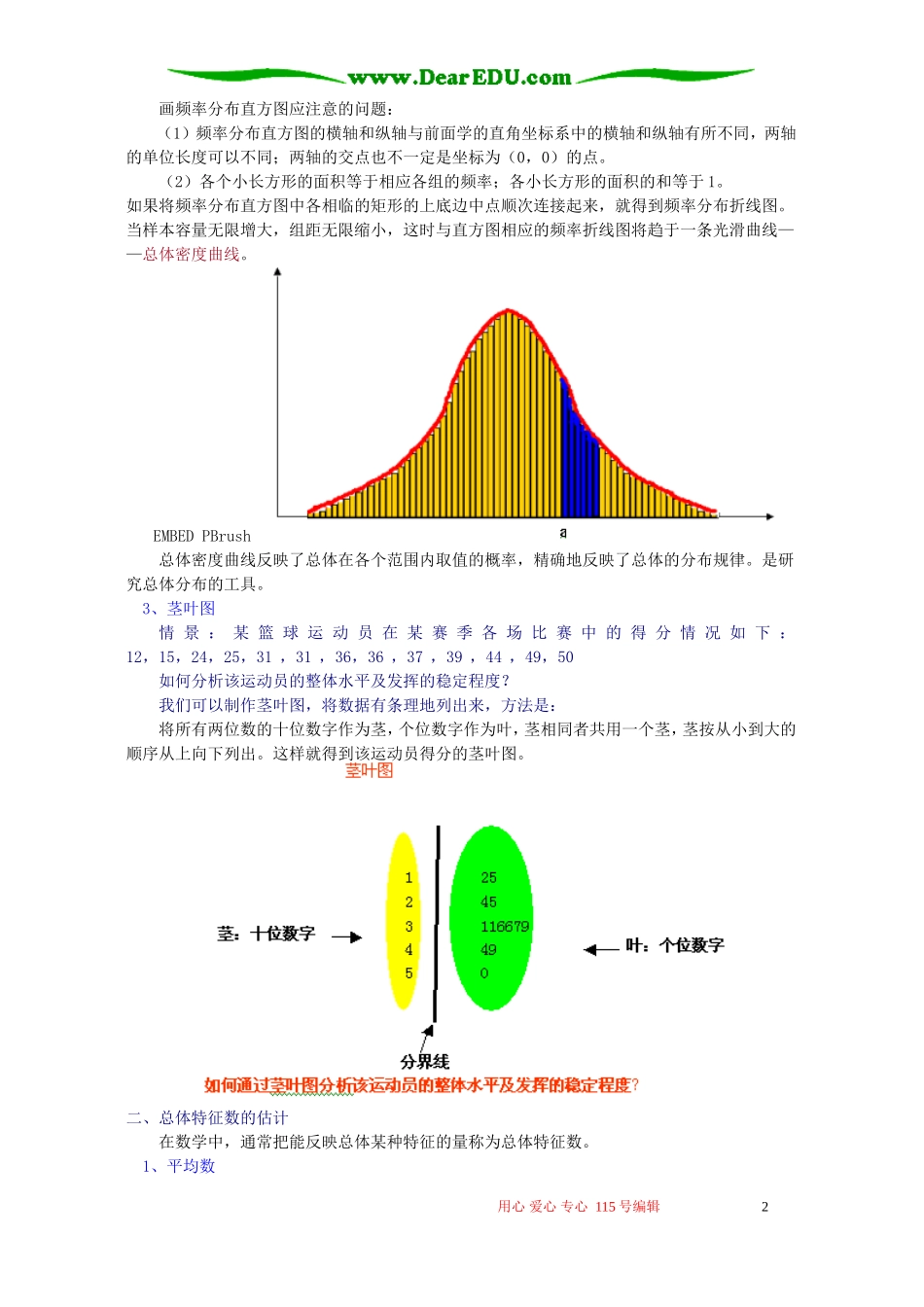
总体分布估计与总体特征数的估计知识精讲一.本周教学内容:总体分布估计与总体特征数的估计[教学目标]1、通过实例的分析,体会分布的意义和作用。在表示样本数据的过程中,学会列频率分布表,画频率直方图、频率折线图和茎叶图2、理解数据标准差的意义和作用,学会计算数据的标准差3、在解决统计的问题中,进一步体会用样本估计总体的思想,学会计算数据的标准差4、掌握利用已有的数据对一般的分布作出估计一、总体分布估计1、频率分布表或频率分布条形图历史上有人通过做抛掷硬币的大量重复试验,得到了如下试验结果:试验结果频数频率正面向上(0)361240.5011反面向上(1)359640.4989说明:(1)频率分布表在数量表示上比较确切,而频率分布条形图比较直观,两者相互补充,使我们对数据的频率分布情况了解得更加清楚。(2)①各长条的宽度要相同;②相邻长条之间的间隔要适当。频率分布表——当总体很大或不便于获得时,可以用样本的频率分布估计总体的频率分布。我们把反映总体频率分布的表格称为频率分布表。全距:我们将取值区间的长度称为全距。分成区间的长度称为组距。编制频率分布表的步骤(1)求全距,决定组数和组距,组距=全距/组数;(2)分组,组内数值所在区间取左闭右开区间,最后一组取闭区间;(3)登记频数,计算频率,列出频率分布表。2、频率分布直方图与折线图画频率分布直方图的步骤:(1)计算最大值与最小值的差(知道这组数据的变动范围)(2)决定组距与组数(将数据分组)组数:将数据分组,当数据在100个以内时,按数据多少常分5-12组。组距:指每个小组的两个端点的距离。(4)决定分点。(5)列出频率分布表。(6)画出频率分布直方图。用心爱心专心115号编辑1画频率分布直方图应注意的问题:(1)频率分布直方图的横轴和纵轴与前面学的直角坐标系中的横轴和纵轴有所不同,两轴的单位长度可以不同;两轴的交点也不一定是坐标为(0,0)的点。(2)各个小长方形的面积等于相应各组的频率;各小长方形的面积的和等于1。如果将频率分布直方图中各相临的矩形的上底边中点顺次连接起来,就得到频率分布折线图。当样本容量无限增大,组距无限缩小,这时与直方图相应的频率折线图将趋于一条光滑曲线——总体密度曲线。EMBEDPBrush总体密度曲线反映了总体在各个范围内取值的概率,精确地反映了总体的分布规律。是研究总体分布的工具。3、茎叶图情景:某篮球运动员在某赛季各场比赛中的得分情况如下:12,15,24,25,31,31,36,36,37,39,44,49,50如何分析该运动员的整体水平及发挥的稳定程度?我们可以制作茎叶图,将数据有条理地列出来,方法是:将所有两位数的十位数字作为茎,个位数字作为叶,茎相同者共用一个茎,茎按从小到大的顺序从上向下列出。这样就得到该运动员得分的茎叶图。二、总体特征数的估计在数学中,通常把能反映总体某种特征的量称为总体特征数。1、平均数用心爱心专心115号编辑2n个实数的和简记为,读作sigma;n个实数的平均数也叫做算术平均数,记作:我们把两数据之间的差称为两数据的“离差”,两相同数据的“离差”可能为正,也可能为负,但绝对值相等。平均数不是描述总体质量、水平的唯一特征数,在两样本平均数相同的情况下并不能代表样本的质量、水平相同。2、方差和标准差三、线性回归方程在实际问题中,变量之间的常见关系有如下两类:1、确定性函数关系:变量之间可以用函数表示2、相关关系:变量之间具有一定的联系,但不能完全用函数表达引入:某小卖部为了了解热茶销售量与气温的大致的关系,随机统计并制作了某6天卖出热茶的杯数与当天气温对照表如果某天的气温是-5℃,你能根据这些数据预测这天小卖部卖出热茶的杯数么?考虑离差的平方和:用心爱心专心115号编辑3一般地,设有n对观察数据如下:仿照前面的方法,可得线性回归方程中系数a,b满足由此二元一次方程组便可依次求出b、a的值。【典型例题】例1.为了了解某地区高三学生的身体发育情况,抽查了地区内100名年龄为17.5岁~18岁的男生的体重情况,结果如下(单位:kg)56.569.56561.564.566.56464.57658.57273.556677057.565.56871756268.562.56659.5...