14.1.1同底数幂的乘法VIP免费

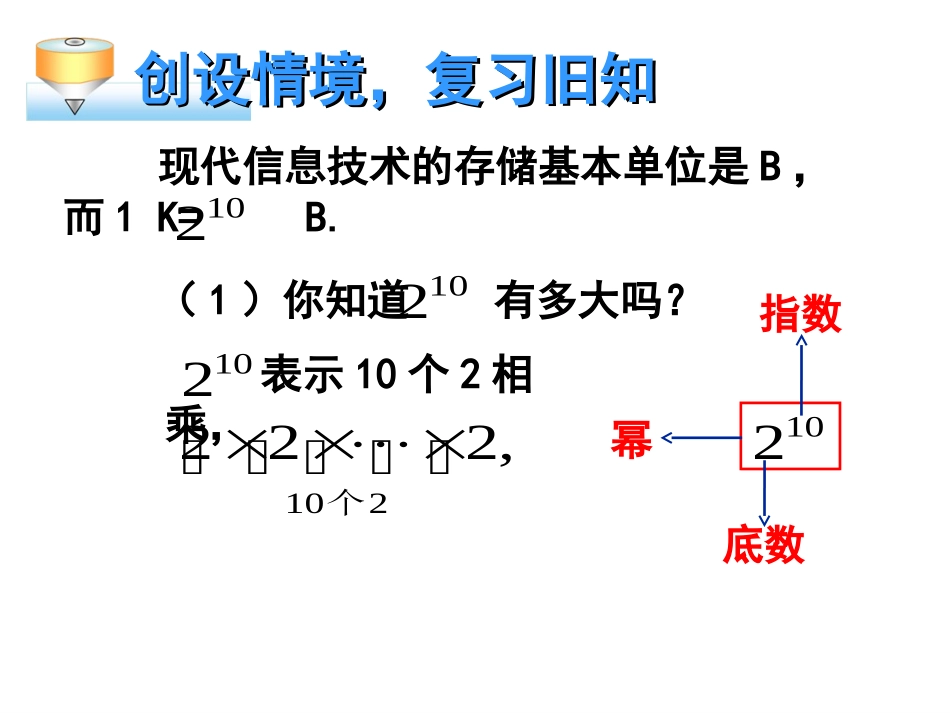
第十四章整式的乘法与因式分解14.114.1整式的乘整式的乘法法14.1.114.1.1同底数幂的乘法同底数幂的乘法创设情境，复习旧知创设情境，复习旧知现代信息技术的存储基本单位是B，而1K=B.（1）你知道有多大吗？,222210个102102102表示10个2相乘，102底数幂指数创设情境，复习旧知创设情境，复习旧知（2）请解释为什么1K≈B.310因为1K=B=1024B≈B.310102102表示个相乘，结果是.表示个相乘，结果是.表示个相乘，结果是.3535na22na，12na.12na125435-2103-5-125练习延续情境，探究新知延续情境，探究新知【例1】现代信息技术的存储单位除了B，K，还常用M,G等.其中1G≈M，1M≈K，1K≈B.那么，1G的U盘容量约能存储多少个K？（按要求列算式并计算）列式：331010310310310延续情境，探究新知延续情境，探究新知列式：3310101.探究算法：331010)101010()101010(101010101010610.下面两式又如何计算呢？nm101035aa延续情境，探究新知延续情境，探究新知2.归纳算法：nmnmaaa(m、n都是正整数）nmaaamaaa个)(anaaa个)(anmaaa个)(nma证明：乘方的意义乘法结合律乘方的意义延续情境，探究新知延续情境，探究新知（1）是什么运算？3.定义法则：nmaa（2）数形式上有什么特点？nmaa、（3）幂有何共同特点？nmaa、（4）所以叫做同底数幂的乘法.nmaa同底数幂相乘，底数不变，指数相加.乘法都是幂的形式底数相同延续情境，探究新知延续情境，探究新知4.运用法则：25(1);xx【例2】计算：6(2);aa43(3)-2-2-2;（）（）（）31(4).mmxx答案：;)1(7x;)2(7a8(3)-2=256;（）.)4(14mx随堂练习：教材第96页练习(1)～(4).变式训练，拓展提高变式训练，拓展提高1.变换底数：【例3】计算：23(1)(5)(5)(5);;)()2(62aa22(3)()();xxx211(4)()(.nnxxn为正整数）分析：关键在于把互为相反数的两个幂化为同底数幂.变式训练，拓展提高变式训练，拓展提高1.变换底数：【例4】计算：;)())(1(53baba;)())()(2(32yxxyyx2(3)()()(nnxyyxn为正整数）.分析：底数可以是多项式，只要能化成同底数就可运用此法则.变式训练，拓展提高变式训练，拓展提高2.变换运算：【例5】计算：;22)1(101021(2)().nnnxxxx区分同底数幂法则与合并同类项法则.变式训练，拓展提高变式训练，拓展提高3.变换题型：【例6】：;,162)1(1的值求如果xx.,125,5)2(的值求如果nmnmaaa回顾小结，课外巩固回顾小结，课外巩固（1）同底数幂的运算法则.（2）运用同底数幂的运算法则时应注意什么？小结：