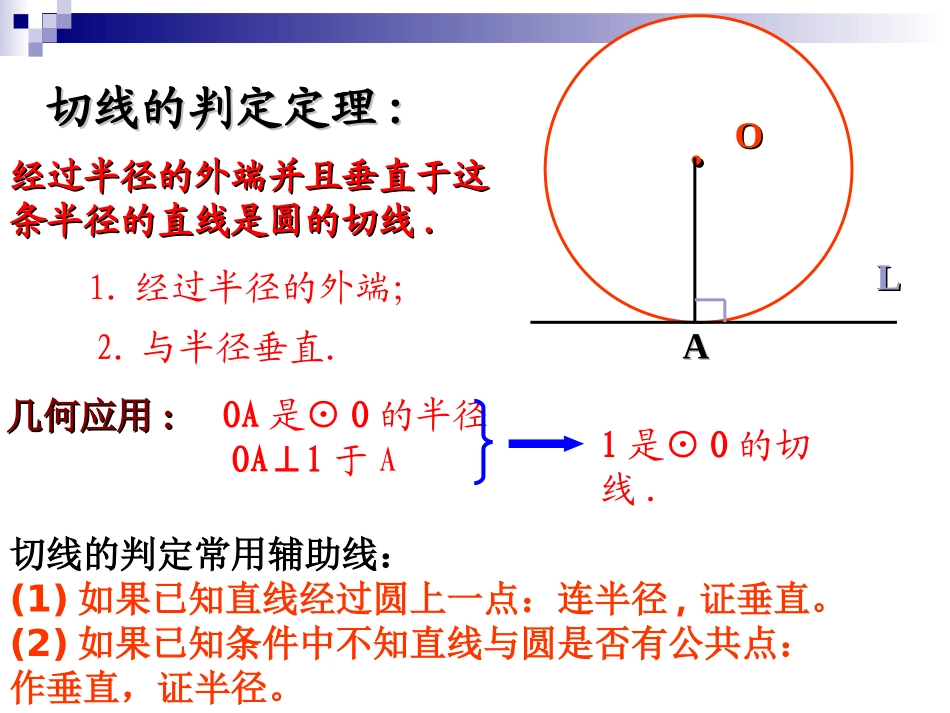
..AAOOLL切线的性质定理切线的性质定理::圆的切线垂直于过切圆的切线垂直于过切点的半径点的半径几何应用几何应用:: LL是⊙是⊙OO的切线,的切线,∴∴OAL⊥OAL⊥过圆上的一点作圆的切线,可以作出几条切线?切线的性质常用辅助线:已知圆的切线和切点时,连半径,得垂直AA..OOLL经过半径的外端并且垂直于这经过半径的外端并且垂直于这条半径的直线是圆的切线条半径的直线是圆的切线..几何应用几何应用::2.与半径垂直.1.经过半径的外端;OA是⊙O的半径OA⊥l于Al是⊙O的切线.切线的判定定理切线的判定定理::切线的判定常用辅助线:(1)如果已知直线经过圆上一点:连半径,证垂直。(2)如果已知条件中不知直线与圆是否有公共点:作垂直,证半径。新课学习新课学习O。ABP在地球外有一颗通讯卫星P,你能画出它发出的信号对地球的最大覆盖区域吗?O。ABP过圆外一点可以引圆的几条切线?尺规作图:过⊙O外一点作⊙O的切线O·PABO在经过圆外一点的切线上,这一点和切点之间的线段的长叫做这点到圆的切线长。·OPAB切线与切线长是一回事吗?它们有什么区别与联系呢?··切线:不可以度量。切线长:可以度量。比一比比一比BOABP思考:已知⊙O切线PA、PB,A、B为切点,把圆沿着直线OP对折,你能发现什么?12PA=PB∠OPA=OPB∠猜想猜想请证明你所发现的结论。APOBPA=PB∠OPA=OPB∠ PA,PB与⊙O相切,点A,B是切点∴OA⊥PA,OB⊥PB即∠OAP=OBP=90°∠ OA=OB,OP=OP∴Rt△AOP≌Rt△BOP(HL)∴PA=PBOPA=OPB∠∠试用文字语言叙述你所发现的结论证一证证一证证明:连接PO、AO、BOPA、PB分别切⊙O于A、BPA=PB∠OPA=OPB∠从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。几何语言:反思:切线长定理为证明线段相等、角相等提供新的方法OPAB切线长定理切线长定理一判断(1)过任意一点总可以作圆的两条切线()(2)从圆外一点引圆的两条切线,它们的长相等。()练习PBOA二填空选择(1)如图:PA,PB切圆于A,B两点,∠APB=50度,连结PO,则∠APO=25°探究:PA、PB是⊙O的两条切线,A、B为切点,直线OP交于⊙O于点D、E,交AB于C。BAPOCED(1)写出图中所有的垂直关系OAPA⊥,OBPB⊥,ABOP⊥(3)写出图中所有相等的线段(2)写出图中与∠OAC相等的角∠OAC=OBC=APC=BPC∠∠∠OA=OB=OD=OE,PA-=PB,AC=BC,AE=BE。PBAO反思:在解决有关圆的切线长的问题时,往往需要我们构建基本图形。(3)连结圆心和圆外一点(2)连结两切点(1)分别连结圆心和切点切线长定理为证明线段相等,角相等,弧相等,垂直关系提供了理论依据。必须掌握并能灵活应用。已知:如图,PA、PB是⊙O的切线,切点分别是A、B,Q为AB上一点,过Q点作⊙O的切线,交PA、PB于E、F点,已知PA=12CM,求△PEF的周长。EAQPFBO易证EQ=EA,FQ=FB,PA=PB∴PE+EQ=PA=12cmPF+FQ=PB=PA=12cm∴周长为24cm例题例题11OPABCDE练习:如果PA=4cm,PD=2cm,试求半径OA的长。x解:设OA=xcm,则PO=+=cm在RtΔOAP中,PA=4cm,由勾股定理得222OPOAPA即:解得:x=PDOD(x+2)22224xx3cm半径OA的长为3cm如图:用两根带有刻度的木条做一个夹角为60°的工具尺,你能用它量出一个圆的半径吗?若量出角的顶点到切点的距离为10cm,试求这个圆半径的近似值。已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径.求证:ACOP∥.证法一.如图.连结AB.PA,PB分别切⊙O于A,B∴PA=PB,∠APO=∠BPO∴OPAB⊥又 BC为⊙O直径∴ACAB⊥∴ACOP∥证法一:有直径,构造直径所对的圆周角;例题讲解例题讲解已知:如图,P为⊙O外一点,PA,PB为⊙O的切线,A和B是切点,BC是直径.求证:ACOP∥.证法二.连结AB,交OP于DPA,PB分别切⊙O于A、B∴PA=PB,∠APO=∠BPO∴AD=BD又 BO=DO∴OD是△ABC的中位线∴ACOP∥D例题讲解例题讲解例1、已知:P为⊙O外一点,PA、PB为⊙O的切线,A、B为切点,BC是直径。求证:AC∥OPPACBEO例题讲解例题讲解证法三.连结AB,设OP与AB弧交于点EPA,PB分别切⊙O于A、B∴PA=PB,∠APO=∠BPO∴OPAB⊥∴=∴∠C=∠POB∴ACOP∥证法三:切线长常用辅助线:连结圆心和切点是解决切线长定理相...