高中数学 导数综合（二） 关注原函数课后练习一 新人教版选修2-2VIP免费

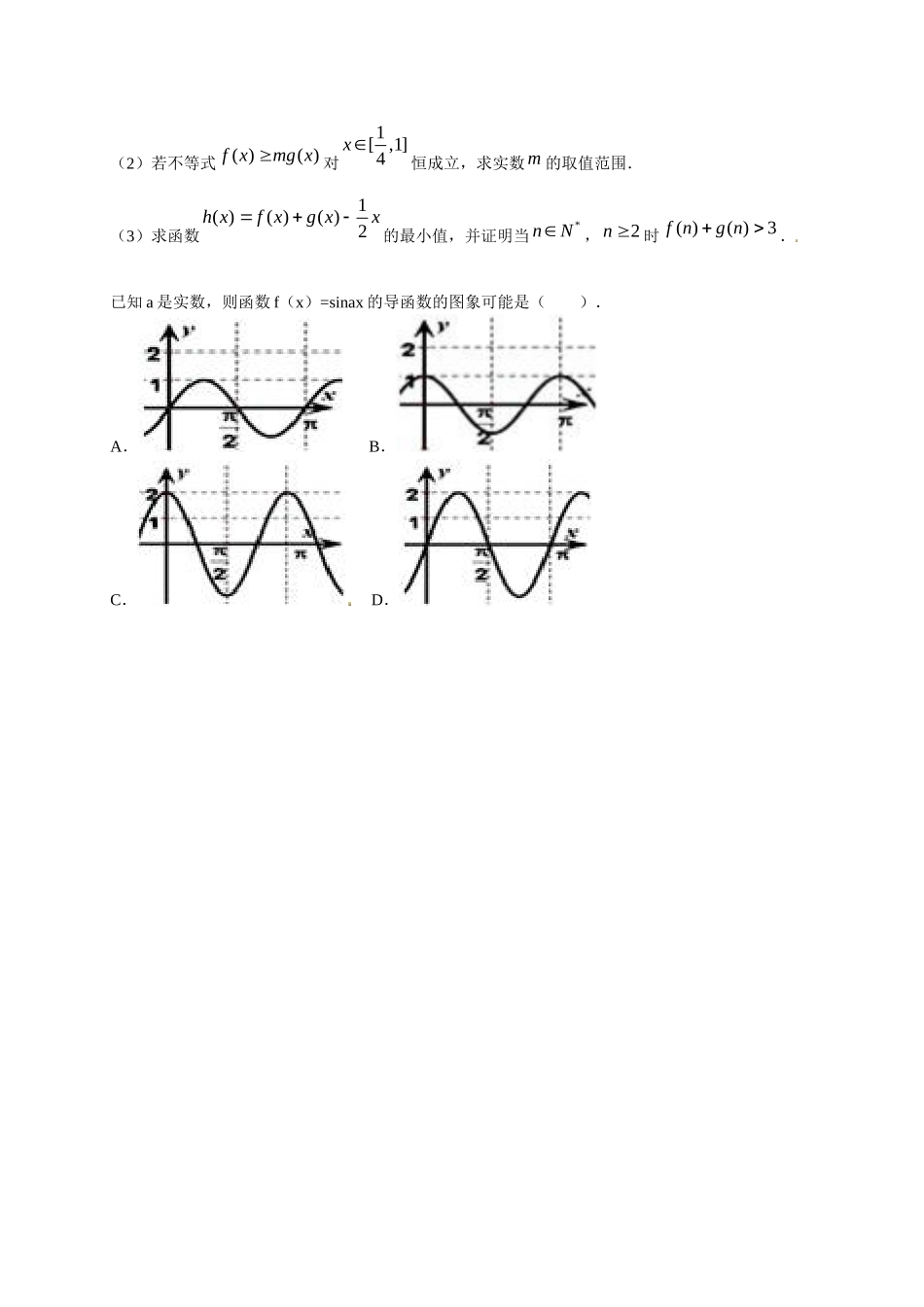
——导数综合（二）关注原函数课后练习（一）已知函数))(1ln()(2Raxaaxxxf（Ⅰ）当1a时，求函数)(xf的最值；（Ⅱ）求函数)(xf的单调区间；（Ⅲ）试说明是否存在实数)1(aa使)(xfy的图象与2ln85y无公共点．已知函数kxxxf2ln)(，（k常数）（1）求函数f(x)的单调区间；（2）若xxf)(恒成立，求k的取值范围．已知函数：()ln3(0)fxxaxa（1）讨论函数()fx的单调性；（2）若对于任意的[1,2]a，若函数23()[2()]2xgxxmfx在区间3,a上有最值，求实数m的取值范围．已知函数21()kxfxxc(0c且1c,kR)恰有一个极大值点和一个极小值点，其中一个是xc．(1)求函数()fx的另一个极值点；(2)求函数()fx的极大值M和极小值m，并求1Mm时，k的取值范围．已知函数2()lnfxxax，()2gxbxx，其中a，bR且2ab．函数()fx在1[,1]4上是减函数，函数()gx在1[,1]4上是增函数．（1）求函数()fx，()gx的表达式；（2）若不等式()()fxmgx对1[,1]4x恒成立，求实数m的取值范围．（3）求函数1()()()2hxfxgxx的最小值，并证明当*nN，2n时()()3fngn．已知a是实数，则函数f（x）=sinax的导函数的图象可能是（）．A．B．C．D．导数综合（——二）关注原函数课后练习参考答案（Ⅰ）)(xf的最小值为3ln24；（Ⅱ）当0a时，)(xf的增区间（1，）；当a>0时，)(xf的减区间为（21,2a），)(xf的增区间为2[,)2a；（Ⅲ）存在．详解：（Ⅰ）函数))(1ln()(2Raxaaxxxf的定义域是（1，）当a=1时，32()12'()2111xxfxxxx，所以)(xf在)23,1(为减函数在),23(为增函数，所以函数)(xf的最小值为33()ln224f．（Ⅱ）22()2'()211axxafxxaxx，若0a时，则22()221,()21axxafxx>0在（1，）恒成立，所以)(xf的增区间（1，）．若122,0aa则，故当]22,1(ax，01)22(2)('xaxxxf，当),22[ax时，01)22(2)(xaxxxf，所以a>0时)(xf的减区间为（22,1a），)(xf的增区间为［),22a．（Ⅲ）1a时，由（Ⅰ）知)(xf在（1，+）的最小值为2ln14)22(2aaaaf，令2ln14)22()(2aaaafag在［1，+）上单调递减，所以2ln43)1()(maxgag，则,081)2ln85()(maxag因此存在实数)1(aa使)(xf的最小值大于2ln85，故存在实数)1(aa使y=)(xf的图象与y=2ln85无公共点．（1）当0k时，f(x)的单调增区间是（0，+）；当k>0时，f(x)的单调增区间是（0，k21），单调减区间是（k21，+）；（2）),21(ee．详解：（1）由kxxxf2ln)(可得，kxxf21)(' )(xf的定义域为（0，+），∴当0k时，021)('kxxf，)(xf在（0，+）是增函数．当k>0时，由021kx可得kx21，∴f(x)在（0，k21）是增函数，在（k21，+）是减函数．综上，当0k时，f(x)的单调增区间是（0，+）；当k>0时，f(x)的单调增区间是（0，k21），单调减区间是（k21，+）．由xxf)(恒成立，可得02lnxkxx恒成立，),0(x．即1ln2,ln2xxkxxkx恒成立．设1ln)(xxxg，则2ln1)('xxxg，令0ln1)('2xxxg得ex．当ex0时，0)(',0)('xgexxg时，当，)(xg在（0，e）上单调递增，在（e，+）上单调递减．1ln)(xxxg在x=e时取得极大值11)(eeg，且为g(x)在（0，+）上的最大值．eekek21,112k的取值范围是),21(ee．（1）当0a时，()fx的单调增区间为1(0,)a，减区间为1(,)a；当0a时，()fx的单调增区间为(0,)，无减区间；（2）321932m．详解：（1）由已知得()fx的定义域为(0,)，且1()fxax，当0a时，()fx的单调增区间为1(0,)a，减区间为1(,)a；当0a时，()fx的单调增区间为(0,)，无减区间；（2）2332()[2()](),22xmgxxmfxxaxx2()3(2)1,gxxmax()gx在区间(,3)a上有最值，()gx在区间(,3)a上不总是单调函数，又()0(0)1(3)0gagg由题意知：对任意22[1,2],()3(2)1510...