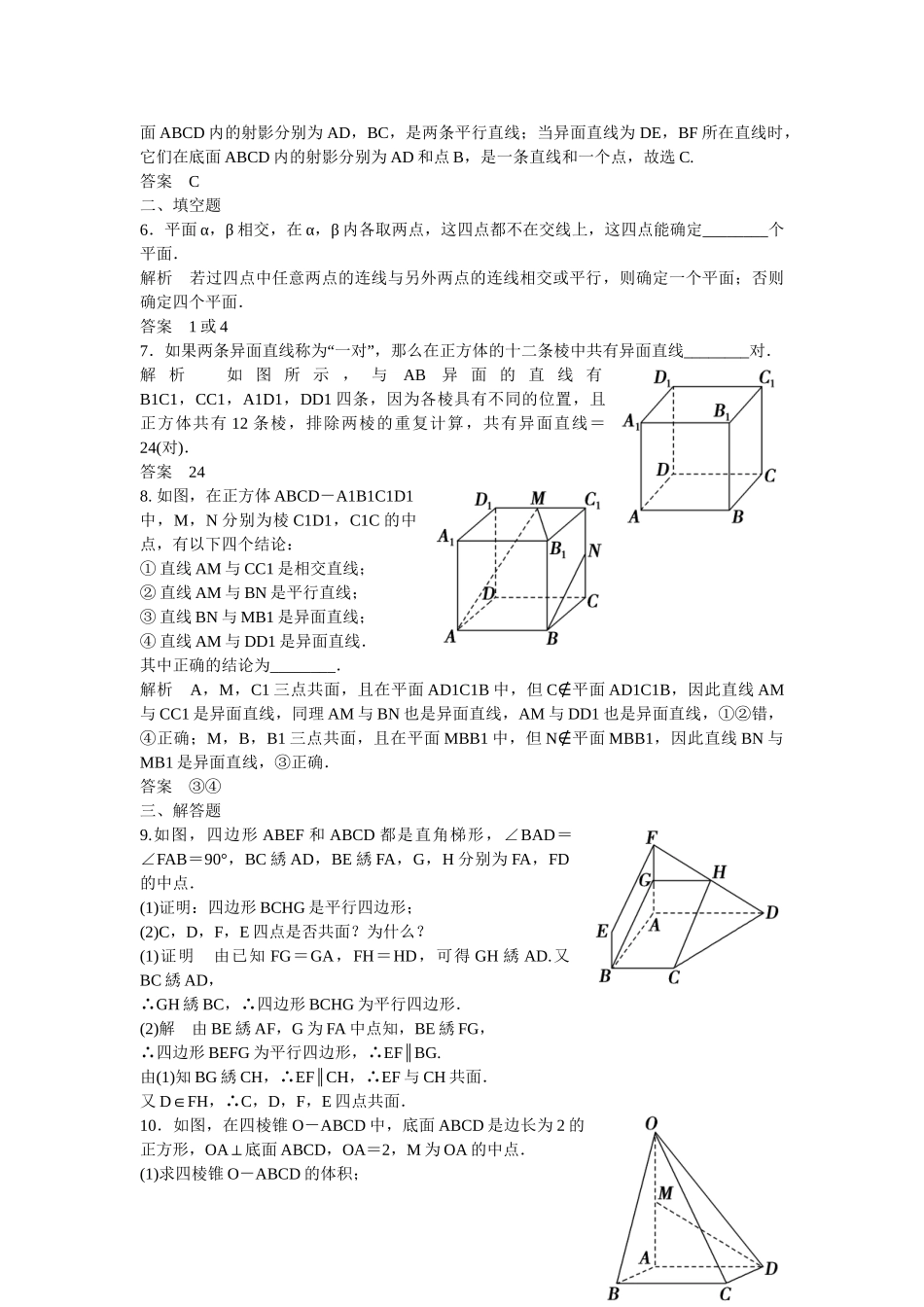
第2讲空间点、线、面的位置关系基础巩固题组(建议用时:40分钟)一、选择题1.若空间三条直线a,b,c满足a⊥b,bc⊥,则直线a与c()A.一定平行B.一定相交C.一定是异面直线D.平行、相交、是异面直线都有可能解析当a,b,c共面时,ac∥;当a,b,c不共面时,a与c可能异面也可能相交.答案D2.(·江西七校联考)已知直线a和平面α,β,α∩β=l,a⊄α,a⊄β,且a在α,β内的射影分别为直线b和c,则直线b和c的位置关系是()A.相交或平行B.相交或异面C.平行或异面D.相交、平行或异面解析依题意,直线b和c的位置关系可能是相交、平行或异面,选D.答案D3.l1,l2,l3是空间三条不同的直线,则下列命题正确的是()A.l1l2⊥,l2l3⊥⇒l1l3⊥B.l1l2⊥,l2l3∥⇒l1l3⊥C.l1l2l3∥∥⇒l1,l2,l3共面D.l1,l2,l3共点⇒l1,l2,l3共面解析当l1l2⊥,l2l3⊥时,l1与l3也可能相交或异面或平行,故A不正确;l1l2⊥,l2l3∥⇒l1l3⊥,故B正确;当l1l2l3∥∥时,l1,l2,l3未必共面,如三棱柱的三条侧棱,故C不正确;l1,l2,l3共点时,l1,l2,l3未必共面,如正方体中从同一顶点出发的三条棱,故D不正确.答案B4.(·三亚一模)在空间四边形ABCD中,AB=CD,AD=BC,AB≠AD,M,N分别是对角线AC与BD的中点,则MN与()A.AC,BD之一垂直B.AC,BD都垂直C.AC,BD都不垂直D.AC,BD不一定垂直解析连接AN,CN, AD=BC,AB=CD,BD=BD,∴△ABD≌△CDB,则AN=CN,在等腰△ANC中,由M为AC的中点知MN⊥AC.同理可证MN⊥BD.故选B.答案B5.(·深圳调研)两条异面直线在同一个平面上的正投影不可能是()A.两条相交直线B.两条平行直线C.两个点D.一条直线和直线外一点解析如图,在正方体ABCD-EFGH中,M,N分别为BF,DH的中点,连接MN,DE,CF,EG.当异面直线为EG,MN所在直线时,它们在底面ABCD内的射影为两条相交直线;当异面直线为DE,GF所在直线时,它们在底面ABCD内的射影分别为AD,BC,是两条平行直线;当异面直线为DE,BF所在直线时,它们在底面ABCD内的射影分别为AD和点B,是一条直线和一个点,故选C.答案C二、填空题6.平面α,β相交,在α,β内各取两点,这四点都不在交线上,这四点能确定________个平面.解析若过四点中任意两点的连线与另外两点的连线相交或平行,则确定一个平面;否则确定四个平面.答案1或47.“”如果两条异面直线称为一对,那么在正方体的十二条棱中共有异面直线________对.解析如图所示,与AB异面的直线有B1C1,CC1,A1D1,DD1四条,因为各棱具有不同的位置,且正方体共有12条棱,排除两棱的重复计算,共有异面直线=24(对).答案248.如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线.其中正确的结论为________.解析A,M,C1三点共面,且在平面AD1C1B中,但C∉平面AD1C1B,因此直线AM与CC1是异面直线,同理AM与BN也是异面直线,AM与DD1也是异面直线,①②错,④正确;M,B,B1三点共面,且在平面MBB1中,但N∉平面MBB1,因此直线BN与MB1是异面直线,③正确.答案③④三、解答题9.如图,四边形ABEF和ABCD都是直角梯形,∠BAD=∠FAB=90°,BC綉AD,BE綉FA,G,H分别为FA,FD的中点.(1)证明:四边形BCHG是平行四边形;(2)C,D,F,E四点是否共面?为什么?(1)证明由已知FG=GA,FH=HD,可得GH綉AD.又BC綉AD,GH∴綉BC,∴四边形BCHG为平行四边形.(2)解由BE綉AF,G为FA中点知,BE綉FG,∴四边形BEFG为平行四边形,∴EFBG.∥由(1)知BG綉CH,∴EFCH∥,∴EF与CH共面.又D∈FH,∴C,D,F,E四点共面.10.如图,在四棱锥O-ABCD中,底面ABCD是边长为2的正方形,OA⊥底面ABCD,OA=2,M为OA的中点.(1)求四棱锥O-ABCD的体积;(2)求异面直线OC与MD所成角的正切值的大小.解(1)由已知可求得,正方形ABCD的面积S=4,所以,四棱锥O-ABCD的体积V=×4×2=.(2)如图,连接AC,设线段AC的中点为E,连接ME,DE,则∠EMD(或其补角)为异面直线OC与MD所成的角,由已知,可得DE=,EM=,MD=, ()2+()2=()2,DEM∴△为直角...