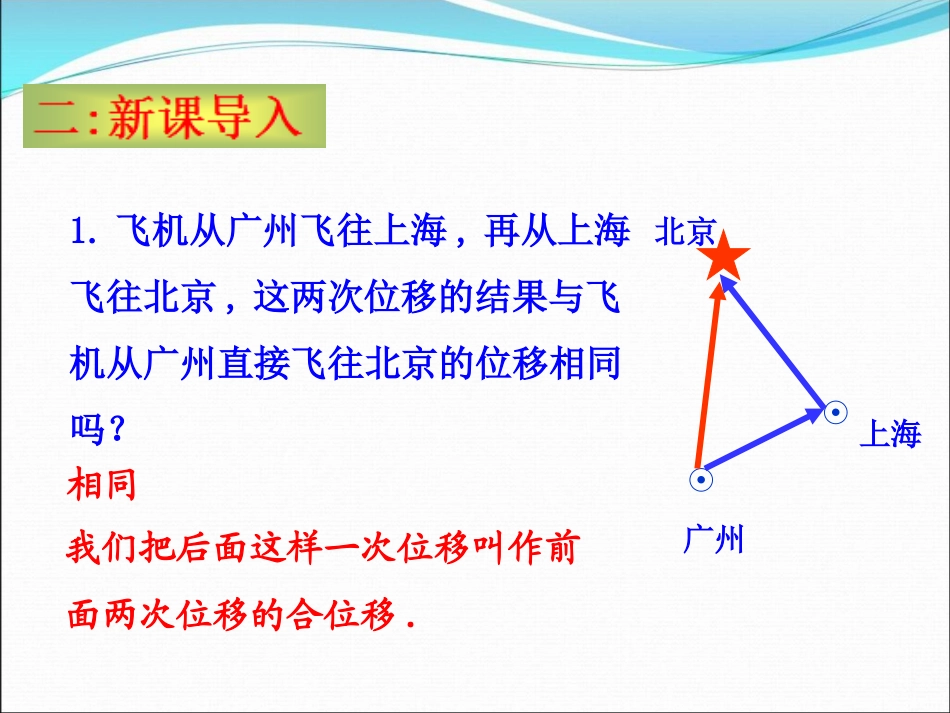
§2.1从位移的合成到向量的加法北师大版高中数学必修4第二章平面向量——太和中学康同芳1.知识与技能:掌握向量加法的定义;会用向量加法的三角形法则和平行四边形法则作两个向量的和向量;2.过程与方法:通过学生熟悉的物理引出向量的加法,启发学生用位移的合成去探索两个向量的和,通过物理背景来去理解向量的加法;3.情感态度与价值观:让学生借助熟悉的物理背景去理解向量加法,激发学生学习数学的兴趣,让学生体会数形结合的数学思想。教学重点:向量加法的三角形法则和平行四边形法则教学难点:向量加法定义的理解北京广州上海1.飞机从广州飞往上海,再从上海飞往北京,这两次位移的结果与飞机从广州直接飞往北京的位移相同吗?我们把后面这样一次位移叫作前面两次位移的合位移.相同ABCD2.在大型生产车间里,一重物被天车从A处搬运到B处.它的实际位移AB,可以看作水平运动的分位移AC与竖直运动的分位移AD的合位移.由分位移求合位移,称为位移的合成.在上一节课中我们知道位移是向量,因此位移合成就是向量的加法,那么向量的加法怎么体现?符合哪些规律呢?这就是我们今天要探究的内容.这种作法叫作向量求和的三角形法则.AC作法:1.在平面内任取一点A.讨论:作图的关键点在哪?首尾顺次相连.B类比前面的广州至北京的飞机位移的合成.(1)同向(2)反向abab思考:(3)规定:ABCBAaCbA思考:类比位移的合成方法,作两向量的和还有没有其他的方法呢?BDCba作法:上述这种方法叫作向量求和的平行四边形法则.思考:这种方法的作图关键点是什么呢?提示:共起点.提升总结:三角形法则和平行四边形法则的使用范围.(1)三角形法则适用于任意两个向量的加法;(2)平行四边形法则适用于不共线的两个向量的加法.例1轮船从A港沿东偏北30°方向行驶了40nmile(海里)到达B处,再由B处沿正北方向行驶40nmile到达C处.求此时轮船与A港的相对位置.北AB30D东C东北AB30CD答:轮船此时位于A港东偏北60°,且距A港40nmile的C处.3数的加法满足交换律与结合律,即对任意a,b∈R,有a+b=b+a,(a+b)+c=a+(b+c).任意向量的加法是否也满足交换律和结合律?a,b向量的加法满足交换律和结合律DACBABCDA1A2+A2A3+A3A4+A4A5+…+An-2An-1+An-1An=思考:能否将它推广至多个向量的求和?A1A2A3A1A2+A2A3+A3A4=_______A1A2+A2A3=_______A1A2A3A4多边形法则:n个首尾顺次相接的向量的和等于折线起点到终点的向量.ABCDEF2.下列非零向量的运算结果为零向量的是()D课堂小结:1.这节课我们学习了哪些知识点?2.在学习的过程中,我们应用了哪些数学思想?数形结合和类比的数学思想.课后作业:课本P81习题5.