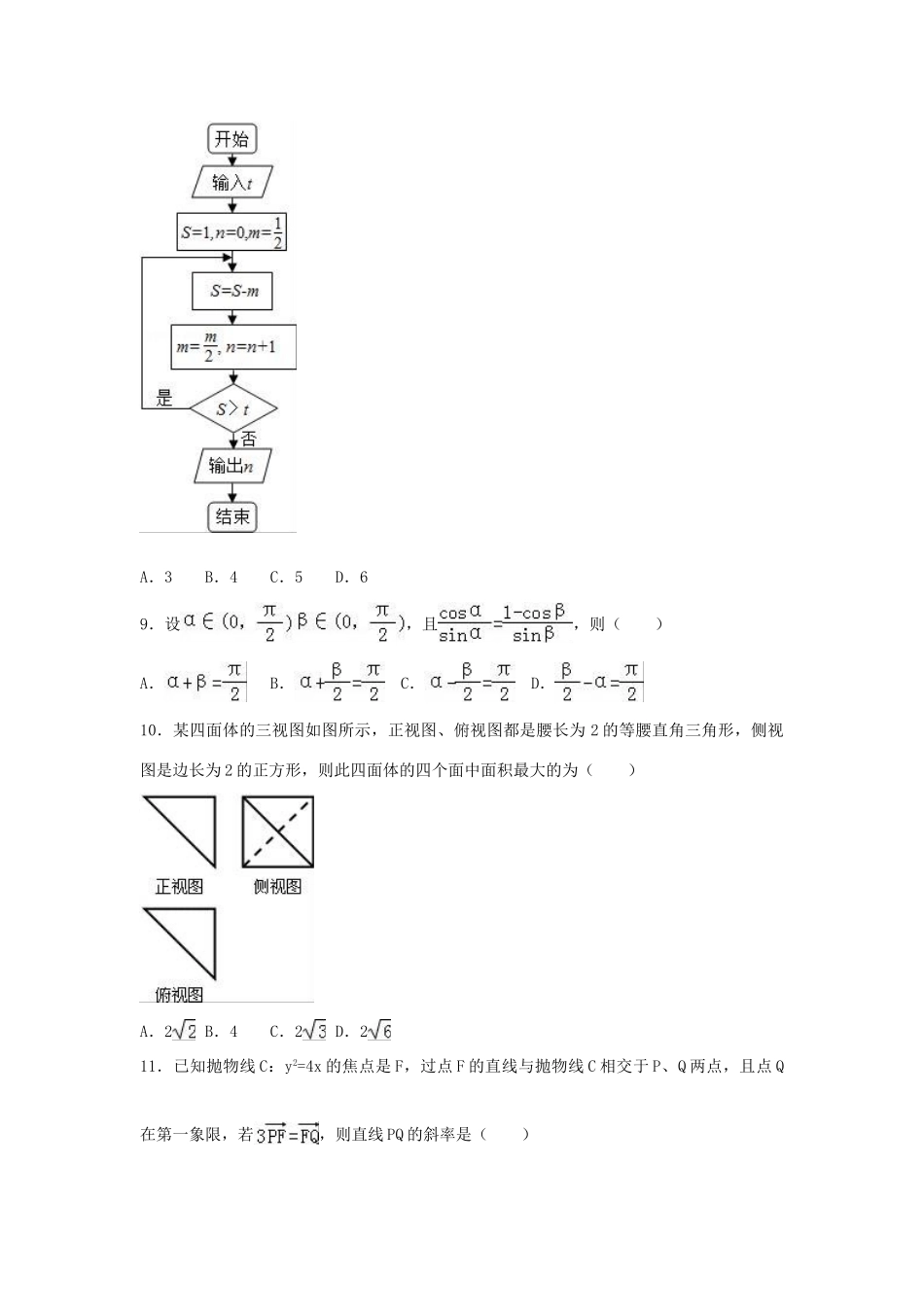
2017年黑龙江省大庆市高考数学模拟试卷(文科)(6)一、选择题:本大题共12小题,每小题5分.1.设全集U=R,集合A={x|1og2x≤2},B={x|(x﹣3)(x+1)≥0},则(∁UB)∩A=()A.(﹣∞,﹣1]B.(﹣∞,﹣1]∪(0,3)C.[0,3)D.(0,3)2.已知复数,则等于()A.B.C.D.3.下列函数中,既是单调函数又是奇函数的是()A.y=log3xB.y=3|x|C.y=D.y=x34.已知双曲线的离心率为,则m的值为()A.B.C.3D.5.若b,c∈[﹣1,1],则方程x2+2bx+c2=0有实数根的概率为()A.B.C.D.6.已知实数x,y满足约束条件,则z=3x+2y的最大值为()A.4B.6C.8D.97.函数f(x)=2x+sinx的部分图象可能是()A.B.C.D.8.执行如图的程序框图,如果输入的t=0.1,则输出的n=()A.3B.4C.5D.69.设,且,则()A.B.C.D.10.某四面体的三视图如图所示,正视图、俯视图都是腰长为2的等腰直角三角形,侧视图是边长为2的正方形,则此四面体的四个面中面积最大的为()A.2B.4C.2D.211.已知抛物线C:y2=4x的焦点是F,过点F的直线与抛物线C相交于P、Q两点,且点Q在第一象限,若,则直线PQ的斜率是()A.B.1C.D.12.荐函数f(x)=lnx+ax2﹣2在区间(,2)内存在单调递增区间,则实数a的取值范围是()A.(﹣∞,﹣2]B.(﹣,+∞)C.(﹣2,﹣)D.(﹣2,+∞)二、填空题:本大题共4小题,每小题5分.13.在△ABC中,a=3,b=4,cosB=,则sinC=.14.甲乙丙三人代表班级参加校运会的跑步,跳远,铅球比赛,每人参加一项,每项都要有人参加,他们的身高各不同,现了解到已下情况:(1)甲不是最高的;(2)最高的是没报铅球;(3)最矮的参加了跳远;(4)乙不是最矮的,也没参加跑步.可以判断丙参加的比赛项目是.15.在平行四边形ABCD中,AD=4,∠BAD=,E为CD中点,若•=4,则AB的长为.16.已知三角形ABC中,角A、B、C所对边分别为a、b、c,满足且,则三角形ABC面积的最大值为.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.已知各项均为正数的数列{an}的前n项和为Sn,a1>1,且,n∈N*.(Ⅰ)求数列{an}的通项公式an;(Ⅱ)若,求数列的前n项和Tn.18.小明同学在寒假社会实践活动中,对白天平均气温与某家奶茶店的A品牌饮料销量之间的关系进行了分析研究,他分别记录了1月11日至1月15日的白天气温x(°C)与该奶茶店的A品牌饮料销量y(杯),得到如下表数据:日期1月11日1月12日1月13日1月14日1月15日平均气温x(℃)91012118销量y(杯)2325302621(Ⅰ)若先从这五组数据中抽出2组,求抽出的2组书记恰好是相邻2天数据的概率;(Ⅱ)请根据所给五组书记,求出y关于x的线性回归方程式.(Ⅲ)根据(Ⅱ)所得的线性回归方程,若天气预报1月16号的白天平均气温为7(℃),请预测该奶茶店这种饮料的销量.(参考公式:==,=﹣x)19.三棱柱ABC﹣A1B1C1的底面是边长为2的等边三角形,AA1⊥底面ABC,点E,F分别是棱CC1,BB1上的点,且EC=B1F=2FB.(1)证明:平面AEF⊥平面ACC1A1;(2)若AA1=3,求直线AB与平面AEF所成角的正弦值.20.已知椭圆的离心率是,上顶点B是抛物线x2=4y的焦点.(Ⅰ)求椭圆M的标准方程;(Ⅱ)若P、Q是椭圆M上的两个动点,且OP⊥OQ(O是坐标原点),由点O作OR⊥PQ于R,试求点R的轨迹方程.21.设函数f(x)=x﹣lnx+,曲线y=f(x)在x=1处的切线为y=2.(1)求函数f(x)的单调区间;(2)当x∈[1,4]时,证明:f(x)>f′(x)+.[选修4-4:坐标系与参数方程]22.已知曲线C的极坐标方程为,以极点为平面直角坐标系的原点,极轴为x轴的正半轴建立平面直角坐标系.(1)求曲线C的普通方程;(2)A、B为曲线C上两个点,若OA⊥OB,求的值.选考题(共1小题,满分0分)23.已知函数f(x)=|2x﹣a|+a.(1)当a=2时,求不等式f(x)≤6的解集;(2)设函数g(x)=|2x﹣1|,当x∈R时,f(x)+g(x)≥3,求a的取值范围.2017年黑龙江省大庆实验中学高考数学模拟试卷(文科)(6)参考答案与试题解析一、选择题:本大题共12小题,每小题5分.1.设全集U=R,集合A={x|1og2x≤2},B={x|(x﹣3)(x+1)≥0},则(∁UB)∩A=()A.(...