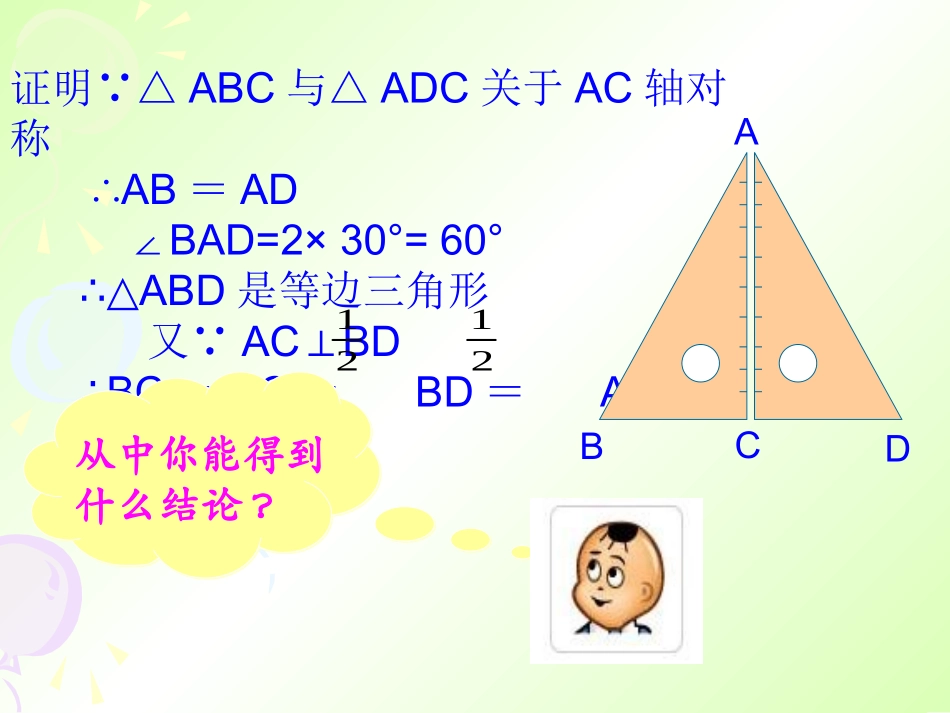
义务教育课程标准实验教科书八年级(上册)八年级数学第十四章轴对称等边三角形BACD将两个含有板有30°的三角尺如图摆放在一起,你能借助这个图形,找到RtABC△的直角边BC与斜边AB之间的数量关系吗?我能行33证明∵△ABC与△ADC关于AC轴对称∴AB=AD∠BAD=2×30°=60°∴△ABD是等边三角形又∵ACBD⊥∴BC=DC=BD=AB从中你能得到什么结论?BACD2121定理:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.在RtABC△中∵∠A=30°∴AB=2BCABC300这又是一个判定两条线段成倍分关系的根据之一.例1.下图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=7.4m,A∠=30°立柱BC、DE要多长?ABDEC反过来怎么样反过来怎么样————逆向思维逆向思维命题:在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300.是真命题吗?如果是,请你证明它.ABC已知:如图,在△ABC中,∠ACB=900,BC=AB.求证:∠A=300.21反过来怎么样反过来怎么样————逆向思维逆向思维在△ABD中,∵∠ACB=900(已知),∴AB=AD(线段垂直平分线上的点到线段两端的距离相等).又∵BC=AB/2(已知),BC=BD/2(作图),∴AB=BD(等量代换).∴AB=BD=AD(等式性质).∴△ABD是等边三角形(等边三角形定义).∴∠B=600(等边三角形定义).∴∠A=300(直角三角形两锐角互余).300ABCD证明:如图,延长BC至D,使CD=BC,连接AD.几何的几何的三种语言三种语言回顾反思44′这是一个通过线段之间的关系来判定一个角的具体度数(300)的根据之一.定理:在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300.在△ABC中∵∠ACB=900,BC=AB/2(已知),∴∠A=300(在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300).ABC300回味无穷回味无穷•特殊的直角三角形的性质:定理:在直角三角形中,如果有一个锐角等于300,那么它所对的直角边等于斜边的一半.定理:在直角三角形中,如果一条直角边等于斜边的一半,那么它所对的锐角等于300.小结拓展结束寄语结束寄语•证明的规范性在于:条理清晰,因果相应,言必有据.这是初学证明者谨记和遵循的原则.下课了!再见!