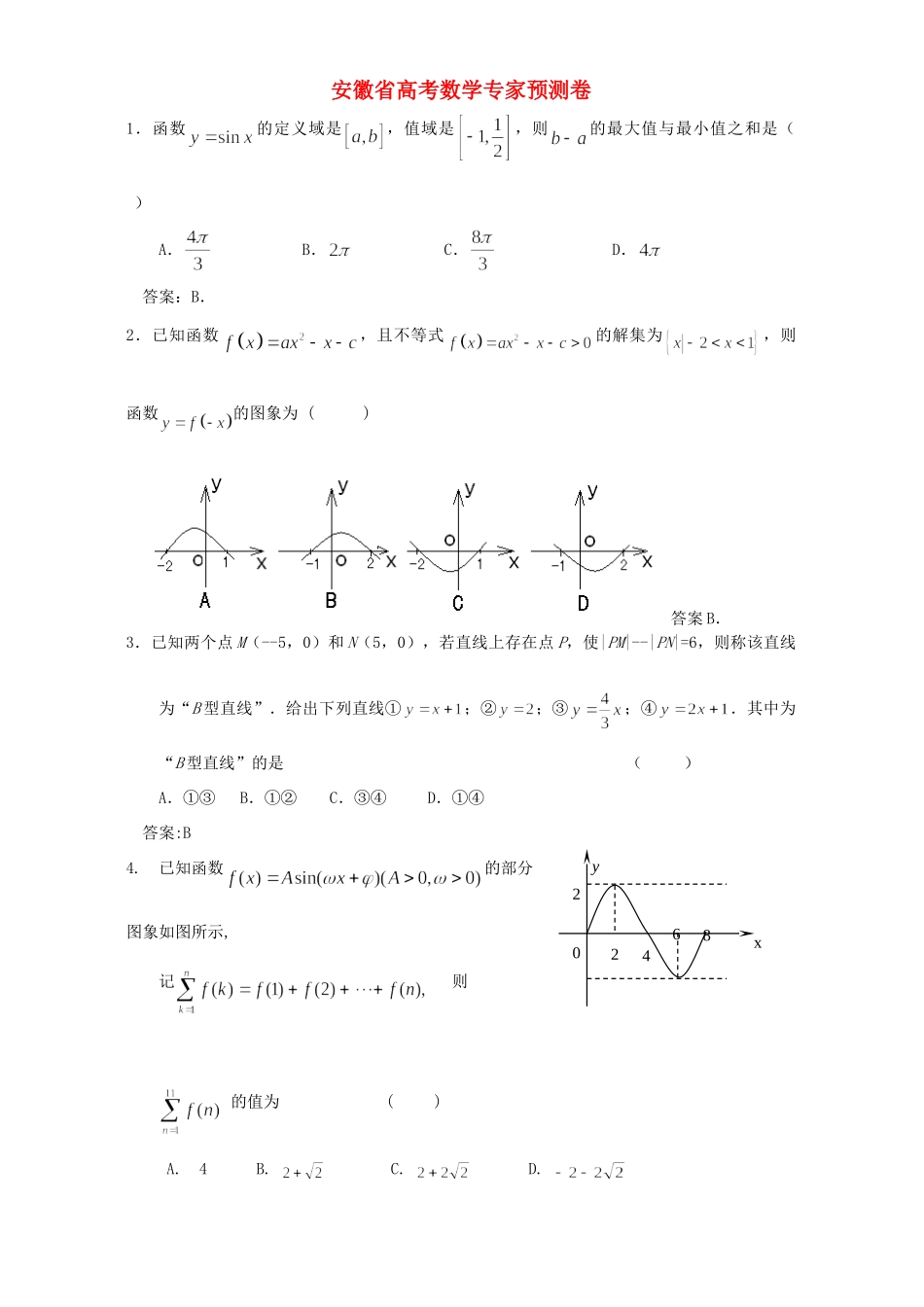
安徽省高考数学专家预测卷1.函数的定义域是,值域是,则的最大值与最小值之和是()A.B.C.D.答案:B.2.已知函数,且不等式的解集为,则函数的图象为()答案B.3.已知两个点M(--5,0)和N(5,0),若直线上存在点P,使|PM|--|PN|=6,则称该直线为“B型直线”.给出下列直线①;②;③;④.其中为“B型直线”的是()A.①③B.①②C.③④D.①④答案:B4.已知函数的部分图象如图所示,记则的值为()A.4B.C.D.xy022468故选C.5.已知x轴上有一列点P1,P2,P3,…,Pn,…,当时,点Pn是把线段Pn-1Pn+1作n等分的分点中最靠近Pn+1的点,设线段P1P2,P2P3,…,PnPn+1的长度分别为,其中.(1)写出和(,)的表达式;(2)证明:();(1)设点在这些点中是否存在两个点同时在函数的图象上,如果存在,请求出点的坐标;如果不存在,请说明理由.解析:(1)由已知令令同理:所以(2)因为所以而时,成立,所以(3)假设有两个点A(,且,都在函数上,即所以消去k得,……①以下考查数列的增减情况,,当时,>0,所以对于数列有∴不可能存在p,q使得①式成立,因而,不存在.6.点P(-3,1)在椭圆的左准线上.过点P且方向为a=(2,-5)的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为()A.B.C.D.答案A.7..已知棱长为1的正方体容器ABCD-A1B1C1D1,在棱AB,BB1以及BC1的中点处各有一个小孔E、F、G,若此容器可以任意放置,则该容器可装水的最大容积为()A.B.C.D.答案:D8.函数f(x)=logax(a>0,a≠1),若f(x1)-f(x2)=1,则等于()A.2B.1C.D.loga2答案:A9.(理科做)符号表示不超过的最大整数,如,定义函数,那么下列命题中正确的序号是.(1)函数的定义域为R,值域为;(2)方程,有无数解;(3)函数是周期函数;(4)函数是增函数.答案:(2)、(3).10.已知等式成立,则的值等于.yxoP(-3,1)QF1F2y=-2DCBEFGB1A1C1D1A答案:11.自点A(0,-1)向抛物线C:作切线AB,切点为B,且B在第一象限,再过线段AB的中点M作直线与抛物线C交于不同的两点E、F.直线AF、AE分别交抛物线C于P、Q两点.(1)求切线AB的方程及切点B的坐标.(2)证明.解:(1)设切线AB的方程为,代入得,由得,AB的方程为,易得切点B(1,1).(2)线段AB的中点M,设过点M的直线的方程为,与交于由,有.再设P,Q,要证,只要PQ∥AB,证即可.由. A、P、F三点共线,有,∴,∴,又∴同理由A、E、Q三点共线得∴所以PQ∥AB,有.12.若函数满足,且时,则函数的图象与函数的图象的交点个数为()A.16B.18C.20D.无数个答案B.13.已知是三个平面,是两条直线,有下列三个条件:①;②;③.如果命题“且______,则”为真命题,则可以在横线处填入的条件是().A.①或②B.②或③C.①或③D.只有②答案C.14.已知,,则代数式的最小值为()A.B.C.D.答案D15.斜边长为2a的直角三角板ABC的直角顶点C在桌面上,斜边AB与桌面平行,,三角板ABC与桌面所成的锐角为,则边AC的中点到桌面的距离是()A.B.C.D.答案:D16.如图,一条螺旋线是用以下方法画成:是边长为1的正三角形,曲线,,分别以、、为圆心,、、为半径画的弧,曲线称为螺旋线旋转一圈。然后又以为圆心为半径画弧…,这样画到第圈,则所得螺旋线的长度.(要求用含π、的代数式表示即可)A3A2A1CAB第16题图答案:.17.设函数的图象为,将向右平移个单位,可得曲线,若曲线与函数的图象关于轴对称,那么可以是.答案:.18已知△ABC的三个顶点的坐标分别为A(3,3)、B(-3,0)、C(6,0),且G是△ABC的重心,则的余弦值为.答案:19已知函数f(x)的定义域为D,且f(x)同时满足以下条件:(Ⅰ)f(x)在D上单调递增或单调递减(Ⅱ)存在区间[a,b]D,使得f(x)在区间[a,b]上的值域是[a,b]那么我们把函数f(x)(xD)叫闭函数(1)求闭函数y=符合条件(Ⅱ)的区间[a,b];(2)判断函数y=2x-lgx是不是闭函数?若是,请说明理由,并找出区间[a,b];若不是,请说明理由;(3)若y=k+是闭函数,求实数k的取值范围.解析.(1)区间为[-1,1](2)取x=0.01,则y=2.02取x=1,则y=2取x=10,则y=19所以y=2x-lgx在(0,+∞)不满足条件(Ⅰ),不是闭函数(3)y=k...