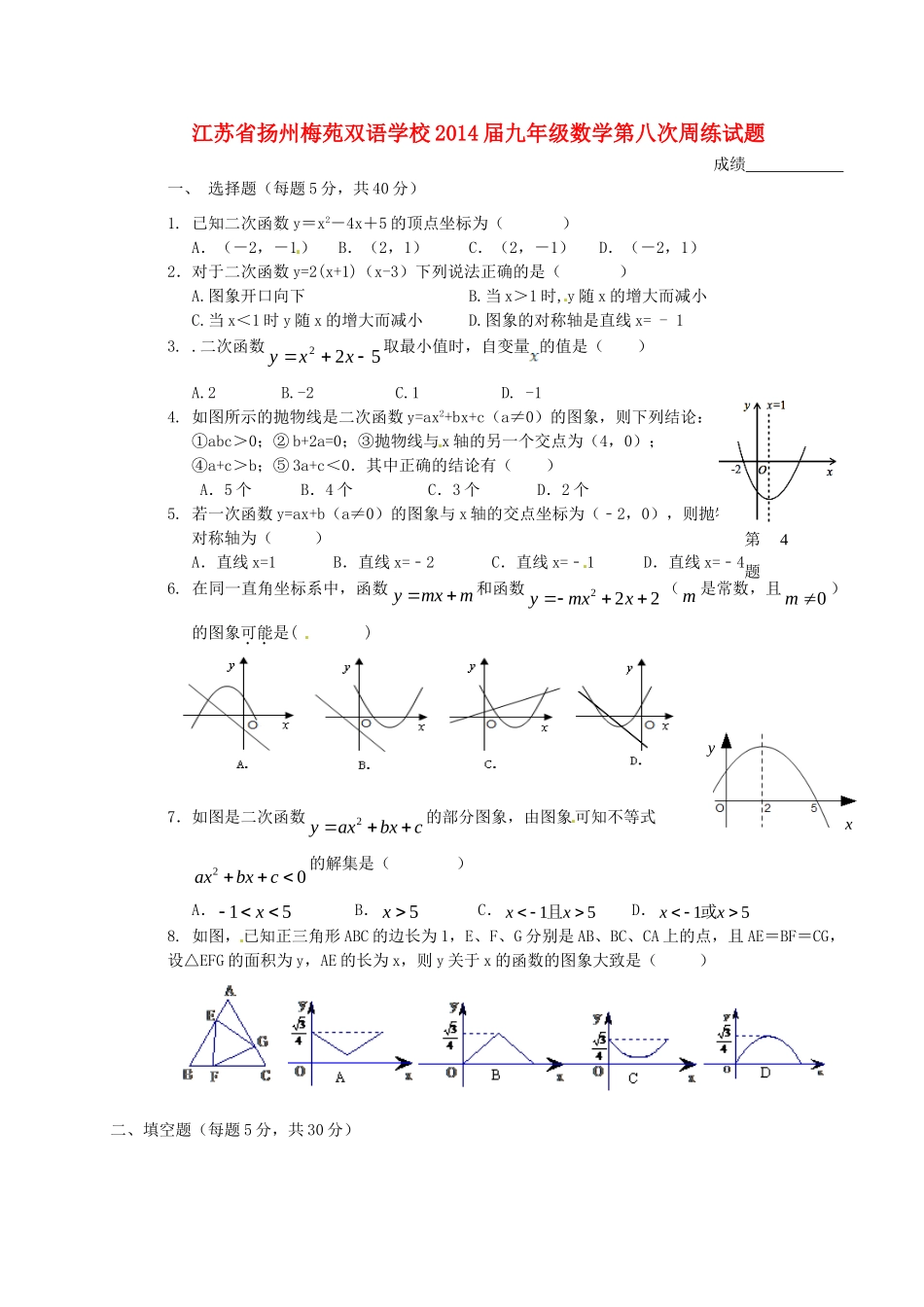
江苏省扬州梅苑双语学校2014届九年级数学第八次周练试题成绩一、选择题(每题5分,共40分)1.已知二次函数y=x2-4x+5的顶点坐标为()A.(-2,-1)B.(2,1)C.(2,-1)D.(-2,1)2.对于二次函数y=2(x+1)(x-3)下列说法正确的是()A.图象开口向下B.当x>1时,y随x的增大而减小C.当x<1时y随x的增大而减小D.图象的对称轴是直线x=-13..二次函数522xxy取最小值时,自变量的值是()A.2B.-2C.1D.-14.如图所示的抛物线是二次函数y=ax2+bx+c(a≠0)的图象,则下列结论:①abc>0;②b+2a=0;③抛物线与x轴的另一个交点为(4,0);④a+c>b;⑤3a+c<0.其中正确的结论有()A.5个B.4个C.3个D.2个5.若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(﹣2,0),则抛物线y=ax2+bx的对称轴为()A.直线x=1B.直线x=﹣2C.直线x=﹣1D.直线x=﹣46.在同一直角坐标系中,函数ymxm和函数222ymxx(m是常数,且0m)的图象可能是()7.如图是二次函数2yaxbxc的部分图象,由图象可知不等式20axbxc的解集是()A.15xB.5xC.15xx且D.15xx或8.如图,已知正三角形ABC的边长为1,E、F、G分别是AB、BC、CA上的点,且AE=BF=CG,设△EFG的面积为y,AE的长为x,则y关于x的函数的图象大致是()二、填空题(每题5分,共30分)yx第4题9.已知二次函数2yx3xm(m为常数)的图象与x轴的一个交点为(1,0),则关于x的一元二次方程2x3xm0的两实数根是_________________.10.二次函数y=x2+1中,当-1<x≤3时,函数y的取值范围为___________.11.将一条长为20cm的铁丝剪成两段,并以每一段铁丝的长度为周长各做成一个正方形,则这两个正方形面积之和的最小值是cm2.12.某种火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式h=-5t2+150t+10表示.经过______s,火箭达到它的最高点.。12.将抛物线221216yxx绕它的顶点旋转180°,所得抛物线的解析式是___13.已知二次函数,当取任意实数时,都有,则的取值范围是______二、解答题(共30分)14.(本题12分)如图所示,二次函数y=﹣x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.(1)求m的值;(2)求点B的坐标;15.(本题8分)某公园草坪的防护栏由100段形状相同的抛物线形构件组成,为了牢固起见,每段护栏需间距0.4m加设一根不锈钢的支柱,防护栏的最高点距底部0.5m(如图所示),请计算所需不锈钢立柱的总长度。16.(本题10分)某公司营销A,B两种产品,根据市场调研,发现如下信息:信息1:销售A种产品所获利润y(万元)与所售产品x(吨)之间存在二次函数关系2y=axbx。当x=1时,y=1.4;当x=3时,y=3.6。信息2:销售B种产品所获利润y(万元)与所售产品x(吨)之间存在正比例函数关系y=0.3x。根据以上信息,解答下列问题:(1)求二次函数解析式;(2)该公司准备购进A,B两种产品共10吨,请设计一个营销方案,使销售A,B两种产品获得的利润之和最大,最大利润是多少?