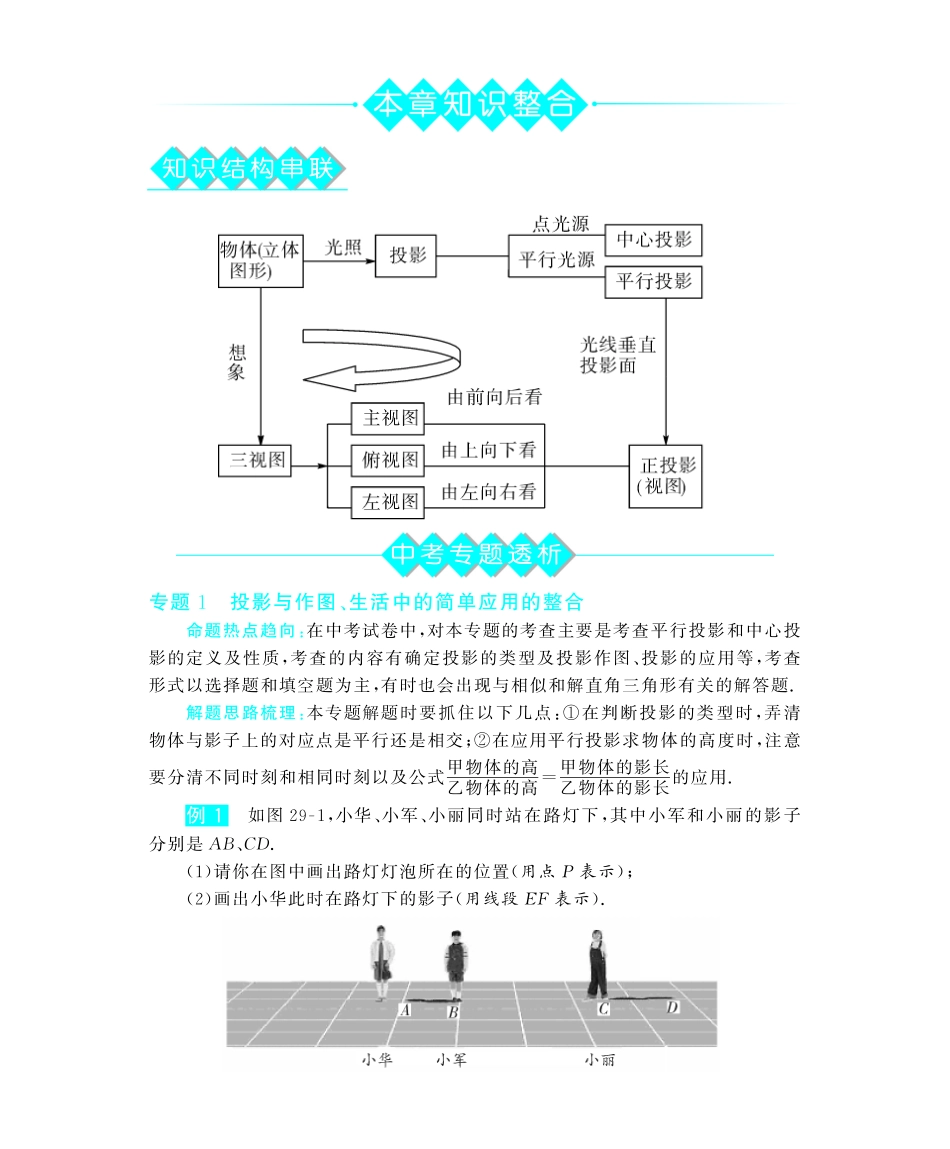
知识结构串联中考专题透析专题1投影与作图、生活中的简单应用的整合命题热点趋向:在中考试卷中,对本专题的考查主要是考查平行投影和中心投影的定义及性质,考查的内容有确定投影的类型及投影作图、投影的应用等,考查形式以选择题和填空题为主,有时也会出现与相似和解直角三角形有关的解答题.解题思路梳理:本专题解题时要抓住以下几点:①在判断投影的类型时,弄清物体与影子上的对应点是平行还是相交;②在应用平行投影求物体的高度时,注意要分清不同时刻和相同时刻以及公式甲物体的高乙物体的高=甲物体的影长乙物体的影长的应用.例1如图29G1,小华、小军、小丽同时站在路灯下,其中小军和小丽的影子分别是AB、CD.(1)请你在图中画出路灯灯泡所在的位置(用点P表示);(2)画出小华此时在路灯下的影子(用线段EF表示).精析:由题意可知,因为是在路灯下形成的影子,所以是中心投影,影子应交于一点,所以根据小军和小丽的影子可以确定灯泡的位置,然后就可以画出小华在路灯下的影子.解答:如图29G2所示:图29G2点拨:在日常生活中,物体在太阳光下的影子是平行投影,而由各种灯光发出的光线可以看成是从一点发出的,因而物体在灯光下的影子是中心投影.图29G3例2如图29G3,丁轩同学在晚上由路灯AC走向路灯BD,当他走到点P时,发现身后他影子的顶部刚好接触到路灯AC的底部,当他向前再步行20m到达点Q时,发现身前他影子的顶部刚好接触到路灯BD的底部,已知丁轩同学的身高是1.5m,两个路灯的高度都是9m,则两路灯之间的距离是().A.24mB.25mC.28mD.30m精析:由于人与路灯都是垂直于地面,可发现人高与路灯恰好构造成“A”字型的两相似三角形,从而利用相似三角形的性质得到两组对应边成比例,即AP2AP+20=1.59,BQ2BQ+20=1.59,而AP=BQ,将两等式同时左右相加,得2BQ2BQ+20=39,解得BQ=5,从而求出两路灯之间的距离是30m,故选D.解答:D.点拨:由投影光线构造相似的几何模型,并利用相似的性质进一步帮助解决实际问题.例3如图29G4,某一时刻太阳光从教室窗户射入室内,与地面的夹角∠BPC为30°,窗户的部分在教室地面所形成的影长PE为3.5m,窗户的高度AF为2.5m,求窗外遮阳篷外端一点D到窗户上缘的距离AD.(结果精确到0.1m)图29G4精析:已知∠BPC为30°,PE为3.5m,可过点E添加辅助线,构造直角三角形,利用边与角之间的关系求出BF的长,从而求出AB,进而利用Rt△BAD中的边与角之间的三角函数关系求出AD的长.解答:过点E作EG∥AC交BP于点G. EF∥BD,∴四边形BFEG是平行四边形.在Rt△PEG中,PE=3.5,∠P=30°,tan∠EPG=EGEP,∴EG=EPtan∠EPG=3.5×tan30°≈2.02(或EG=736). 四边形BFEG是平行四边形,∴BF=EG=2.02.∴AB=AF-BF=2.5-2.02=0.48(或AB=15-736).又AD∥PE,∴∠BDA=∠P=30°.∴在Rt△BAD中,tan30°=ABAD.∴AD=ABtan30°=0.48×3(或AD=53-72)≈0.8(m).∴所求的距离AD约为0.8m.点拨:物体在阳光下的影长与方向随时间的变化而变化,在同一时刻,不同物体的高度与其在太阳光下的影子长度的比是相同的,解决实际问题的关键是根据题中具体条件进行分析,通过添加适当的辅助线构建直角三角形的几何模型,化繁为简,化难为易,并根据直角三角形中边与角的关系,运用数形结合的思想,解决实际问题.专题2实物原型和三视图知识的整合命题热点趋向:本专题是中考中的必考内容之一,主要考查能根据视图描述几何体的形状或名称,由实物确定或作出视图,以及根据三视图判断构成几何体的小立方体的个数等问题,题型多以选择题、填空题为主,有时也以解答题的形式出现.解题思路梳理:本专题解题时要抓住以下几点:①在画物体的视图时,看见的轮廓画成实线,看不见的轮廓画成虚线;②根据三视图还原几何体时,必须将各个视图对照分析得出几何体的长、宽和高;③画几何体的三个视图时,三个视图的位置是有规定的;④在画几何体的三视图时,三视图的大小也是一定的,一般规则是“长对正,高平齐,宽相等”.例4画出如图29G5所示的立体图的三视图.图29G5精析:按照三视...