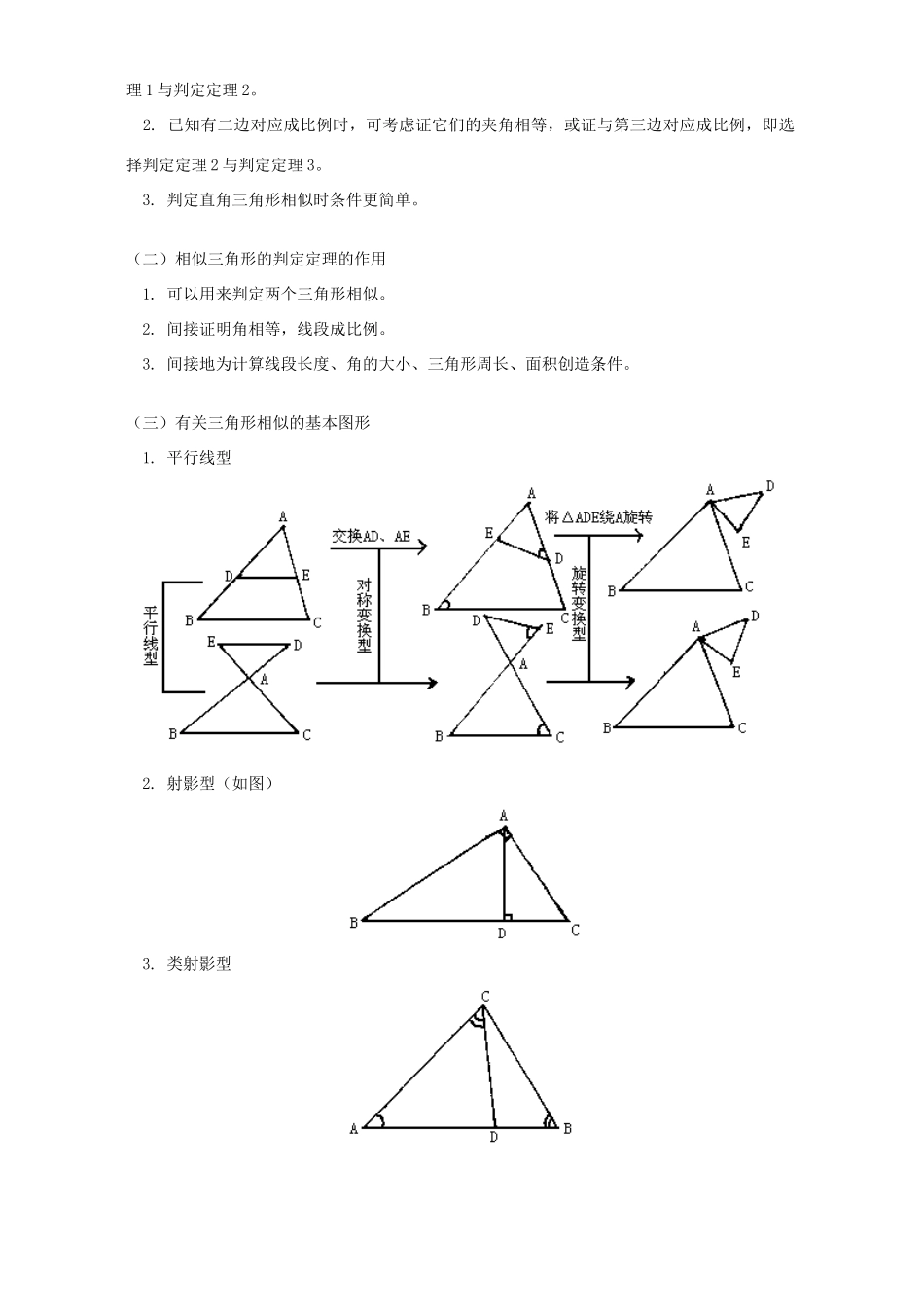
初三数学相似三角形的性质和判定相似多边形位似变换知识精讲一.本周教学内容:相似三角形的性质和判定相似多边形位似变换[教学目标]知识与技能:1.通一些具体的情境和应用,深入对相似三角形的理解和认识;了解相似多边形的含义,并会判断两多边形是否相似;了解位似图形及有关概念。2.初步掌握两个三角形相似的判定条件;理解并掌握相似三角形、相似多边形的性质,并能用来解决简单的问题;能利用作位似图形等方法将一个图形放大或缩小。过程与方法:1.经历对相似三角形的定义的探索和运用过程,进一步体会数学内容之间的内在联系。2.经历两个三角形相似条件的探索过程,进一步发展合情推理能力和初步的逻辑推理意识。3.经历相似多边形概念的形成过程,在探索相似多边形本质特征的过程中,进一步发展学生归纳、类比、反思、交流等方面的能力,提高数学思维水平。4.经历对位似图形及其性质的探索过程,体验用所学的知识解决实际问题。情感、态度与价值观:在探索过程中,体验数学活动充满着探索性和创造性,在学习中进一步提高探究、合作与交流能力,培养学生动手操作的良好习惯。[教学重点]1.相似三角形,及相似多边形的性质和应用。2.相似三角形的判定方法及推理论证的思路。3.位似图形的概念及位似图形的画法及应用。[教学难点]1.应用相似三角形、相似多边形的定义和性质解决实际问题。2.正确运用相似三角形的判定条件找到相似三角形。3.正确理解位似图形的性质。[方法指导](一)怎样选择相似三角形的判定定理:1.已知有一角相等时,可考虑证另一角相等或夹这个角的两边对应成比例,即选择判定定理1与判定定理2。2.已知有二边对应成比例时,可考虑证它们的夹角相等,或证与第三边对应成比例,即选择判定定理2与判定定理3。3.判定直角三角形相似时条件更简单。(二)相似三角形的判定定理的作用1.可以用来判定两个三角形相似。2.间接证明角相等,线段成比例。3.间接地为计算线段长度、角的大小、三角形周长、面积创造条件。(三)有关三角形相似的基本图形1.平行线型2.射影型(如图)3.类射影型(四)判断两个多边形相似,既要看各个角是否对应相等。又要看各边是否对应成比例,两个条件缺一不可。(五)能按要求画出已知图形的位似图形[主要内容](一)相似三角形的性质1.相似三角形对应角相等、对应边成比例。2.相似三角形对应高的比、对应中线的比和对应角平分线的比都等于相似比。3.相似三角形周长的比等于相似比。4.相似三角形面积的比等于相似比的平方。(二)三角形相似的判定方法1.定义法:对应角相等、对应边成比例的两个三角形相似。2.平行法:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。3.判断定理1:两角对应相等的两个三角形相似。4.判定定理2:两边对应成比例且夹角相等的两个三角形相似。5.判定定理3:三边对应成比例的两个三角形相似。6.判定直角三角形相似的方法:……(三)相似多边形的概念及性质1.各角对应相等、各边对应成比例的两个多边形叫做相似多边形。2.相似多边形的性质:相似多边形的周长比等于相似比。相似多边形的面积比等于相似比的平方。(四)位似变换1.定义:取定一点O,把图形每一个点P对应到射线OP(或它的反向延长线)上一点P',使得线段OP'与OP的比等于常数k(k>0),点O对应到它自身,这种变换叫作位似变换。原图形位似的图形。2.位似图形的性质:位似图形上任一对对应点到位似中心的距离之比等于位似比。3.位似图形的画法及步骤:(1)确定位似中心;(2)画经过位似中心,且分别过已知多边形各顶点的直线;(3)分别在各直线上取一点,使其到位似中心的距离与已知多边形的对应顶点到位(4)顺次连接各点。例1.如图,已知△ABC、△DEF为正三角形,D、E分别在AB、AC上,请找一个与△DBE相似的三角形,并证明。分析:应先找到与△DBE相似的三角形,再进行证明。根据条件和图形,同学们不难发现答案不唯一。证明:△DBE与△ECH相似 △ABC与△DEF为等边三角形∴∠B=∠C=60°∴∠BDE+∠BED=120°∠CEH+∠BED=120°∴∠BDE=∠CEH∴△DBE∽△ECH同学们可用类似的方法寻找与...