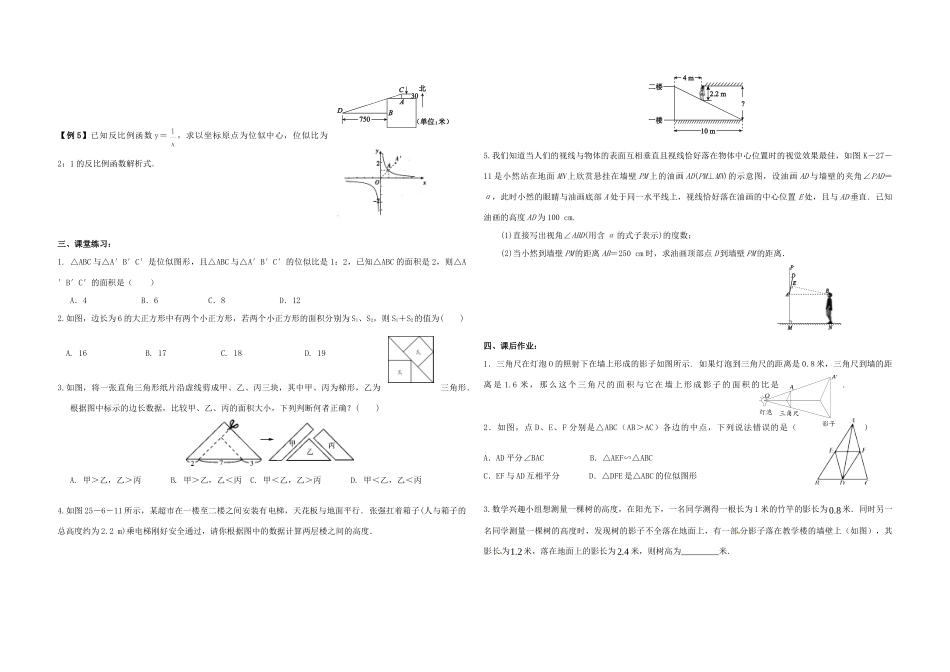
第14讲相似三角形的应用与位似变换姓名:___________一、知识点:观察下图,图中的多边形相似吗?如果相似,那么这种相似有什么共同的特征?1、位似图形的概念:如果两个图形不仅是相似图形,而且每组对应点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心,对应点到位似中心的距离比称为位似比.每对位似对应点与位似中心共线(位似中心可在形上、形外、形内);不经过位似中心的对应线段平行.2、位似变换的作用:利用位似变换可以将一个图形放大或缩小.如:把图中的四边形ABCD缩小到原来的一半.作法一:作法二:作法三:3、位似图形的性质:(1)位似图形上的对应点与位似中心在同一条直线上.(2)位似图形上的对应线段平行或在同一条直线上.(3)位似图形是特殊的相似图形,因此位似图形具有相似图形的一起性质.二、例题讲解:【例1】如图,在正方形ABCD中,点M是BC边上的任一点,连接AM并将线段AM绕M顺时针旋转90°得到线段MN,在CD边上取点P使CP=BM,连接NP、BP.(1)求证:四边形BMNP是平行四边形;(2)线段MN与CD交于点Q,连接AQ,若△MCQ∽△AMQ,则BM与MC存在怎样的数量关系?请说明理由.【例2】如图,□的一边,若的长是的一元二次方程的两个根,.(1)求直线的解析式;(2)若为轴上的点,且,求经过的直线的解析式,并判断与是否相似,并说明理由;(3)若点在平面直角坐标系内,则在直线上是否存在点,使得以为顶点的四边形是菱形,若存在,求点的坐标;若不存在,请说明理由.【例3】如图,正方形OABC的边长为4,点A,C分别在轴和轴的正半轴上,动点P从点A出发,以每秒2个单位长度的速度在线段AB上来回运动,动点Q从点B出发,以每秒1个单位长度的速度沿B-C-O方向向点O运动,P,Q点同时出发,当点Q到达点O时,两点同时停止运动,设运动时间为.(1)当t=1时,求直线PQ的解析式;(2)当点Q在BC上运动时,若以P,B,Q为顶点的三角形与△AOP相似,求的值.【例4】如图,有一所正方形的学校,北门(点A)和西门(点B)分别开在北、西面围墙的正中间.在北门的正北方30米处(点C)有一棵大榕树.如果一个学生从西门出来,朝正西方走750米(点D),恰好见到学校北面的大榕树,那么这所学校占地________平方米.影子三角尺灯泡OAA'【例5】已知反比例函数y=,求以坐标原点为位似中心,位似比为2:1的反比例函数解析式.三、课堂练习:1.△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是2,则△A′B′C′的面积是()A.4B.6C.8D.122.如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1、S2,则S1+S2的值为()A.16B.17C.18D.193.如图,将一张直角三角形纸片沿虚线剪成甲、乙、丙三块,其中甲、丙为梯形,乙为三角形.根据图中标示的边长数据,比较甲、乙、丙的面积大小,下列判断何者正确?()A.甲>乙,乙>丙B.甲>乙,乙<丙C.甲<乙,乙>丙D.甲<乙,乙<丙4.如图25-6-11所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行.张强扛着箱子(人与箱子的总高度约为2.2m)乘电梯刚好安全通过,请你根据图中的数据计算两层楼之间的高度.5.我们知道当人们的视线与物体的表面互相垂直且视线恰好落在物体中心位置时的视觉效果最佳,如图K-27-11是小然站在地面MN上欣赏悬挂在墙壁PM上的油画AD(PM⊥MN)的示意图,设油画AD与墙壁的夹角∠PAD=α,此时小然的眼睛与油画底部A处于同一水平线上,视线恰好落在油画的中心位置E处,且与AD垂直.已知油画的高度AD为100cm.(1)直接写出视角∠ABD(用含α的式子表示)的度数;(2)当小然到墙壁PM的距离AB=250cm时,求油画顶部点D到墙壁PM的距离.四、课后作业:1.三角尺在灯泡O的照射下在墙上形成的影子如图所示.如果灯泡到三角尺的距离是0.8米,三角尺到墙的距离是1.6米,那么这个三角尺的面积与它在墙上形成影子的面积的比是.2.如图,点D、E、F分别是△ABC(AB>AC)各边的中点,下列说法错误的是()A.AD平分∠BACB.△AEF∽△ABCC.EF与AD互相平分D.△DFE是△ABC的位似图形3.数学兴趣小组想测量一棵树的高度,在阳光下,一名同学测得一根长为1米的竹竿...