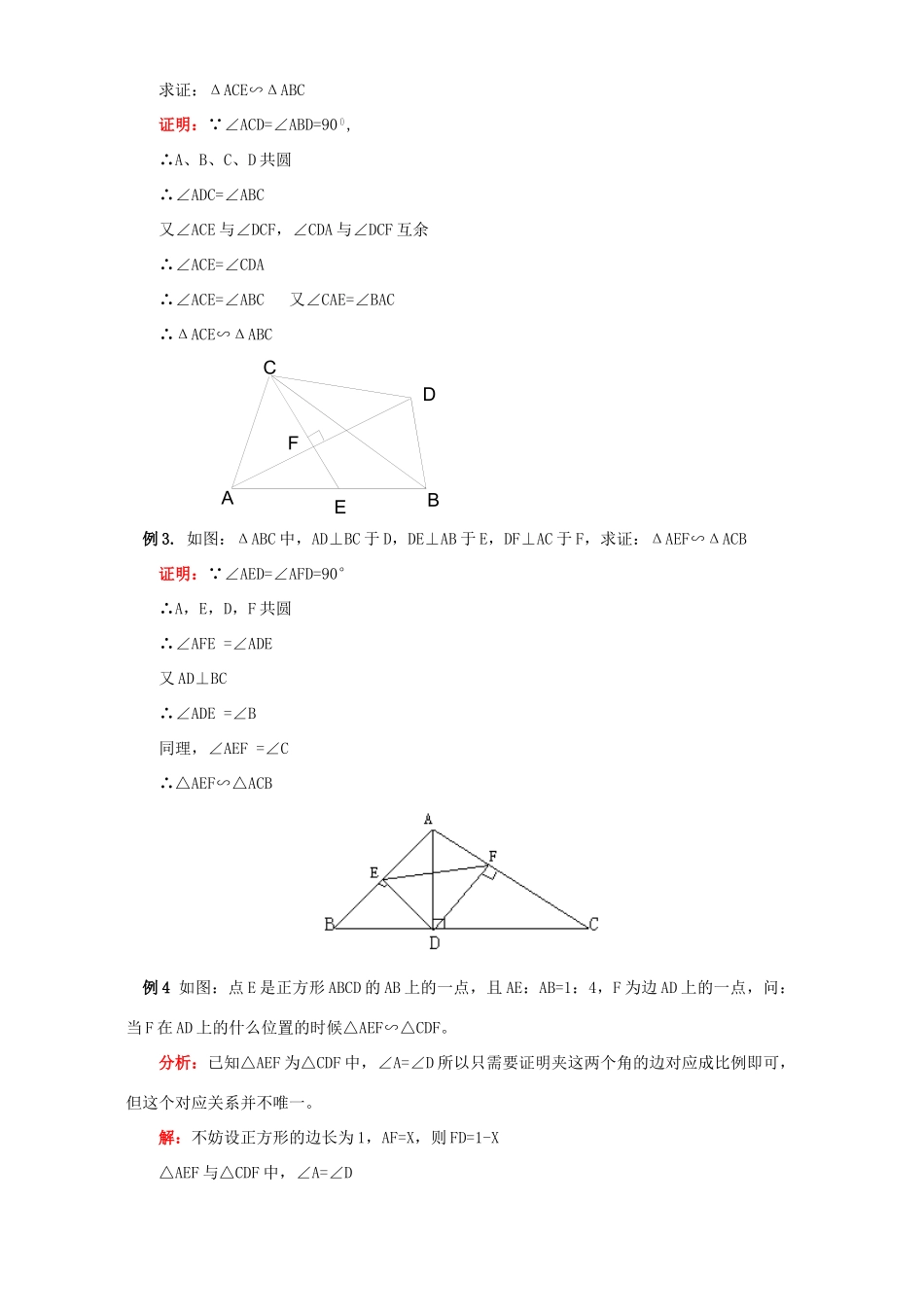
初三数学相似三角形的判定知识精讲一.本周教学内容:相似三角形的判定二.重、难点:怎样选择适当的定理判定三角形的相似是学习中的重点和难点【知识回顾】一.定义:对应角相等,对应边成比例的两个三角形叫相似三角形。相似三角形的对应边的比叫做相似比(也叫相似系数)二.判定:①平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。②两边对应成比例且夹角相等的两个三角形相似。③有两个角对应相等的两个三角形相似。④三条边对应成比例的两个三角形相似。⑤一条直角边和斜边对应成比例的两个直角三角形相似。⑥直角三角形被斜边上的高分成的两个直角三角形与原直角三角形相似。例1.如图:ΔABC中,∠A=60º,BD⊥AC于D,CE⊥AB于E。求证:ΔADE∽ΔABC证明:∵RtΔABD和RtΔACE中,∠A=60º∴∠ABD=∠ACE=30º∴==,又∠A为公共角∴ΔADE∽ΔABC例2.如图:过ΔABC的顶点B和C,分别作AB,AC的垂线BD、CD,使交于点D,过C作CE⊥AD交AB于E,交AD于F求证:ΔACE∽ΔABC证明:∵∠ACD=∠ABD=90,∴A、B、C、D共圆∴∠ADC=∠ABC又∠ACE与∠DCF,∠CDA与∠DCF互余∴∠ACE=∠CDA∴∠ACE=∠ABC又∠CAE=∠BAC∴ΔACE∽ΔABCCAEBDF例3.如图:ΔABC中,AD⊥BC于D,DE⊥AB于E,DF⊥AC于F,求证:ΔAEF∽ΔACB证明:∵∠AED=∠AFD=90°∴A,E,D,F共圆∴∠AFE=∠ADE又AD⊥BC∴∠ADE=∠B同理,∠AEF=∠C∴△AEF∽△ACB例4如图:点E是正方形ABCD的AB上的一点,且AE:AB=1:4,F为边AD上的一点,问:当F在AD上的什么位置的时候△AEF∽△CDF。分析:已知△AEF为△CDF中,∠A=∠D所以只需要证明夹这两个角的边对应成比例即可,但这个对应关系并不唯一。解:不妨设正方形的边长为1,AF=X,则FD=1-X△AEF与△CDF中,∠A=∠D若△AEF∽△CDF,则或成立。即或成立解之,得x=或x=∴当AF=FD=1∶4或AF∶FD=1∶1时,ΔAEF∽ΔCDF(答题时间:30分钟)1.判断下列各命题的真假(真命题打“T”,否则打“F”)(1)若一条直线截三角形的两边所得的三角形与原三角形相似,则这条直线平行于三角的第三边()(2)有一个锐角相等的两个等腰三角形必定相似。()(3)三组边分别平行的两个三角形必定相似。()(4)有一个锐角相等的两个直角三角形必定相似。()(5)一顶角为40º的等腰三角形和一个底角为70º的等腰三角形相似。()(6)四个角对应相等的两个梯形必定相似。()(7)所有的菱形均相似。()(8)所有的正方形均相似。()2.ΔABC中,∠ACB=90º,CD⊥AB于D,DE⊥AC于E,则与ΔABC相似而不全等的三角形的个数是()A.2B.3C.4D.53.已知ΔABC∽ΔA′B′C′,相似比为4,ΔA′B′C′∽ΔA″B″C″,相似比为3,试问:ΔA″B″C″与ΔABC是否相似?若它们相似,则相似比为多少?4.如图,若∠EBC=∠ABD,∠ECB=∠DAB,求证:ΔABC∽ΔDBE。ABECD5.如图,平行四边形ABCD中,AD=10,DC=6,E为AB中点,F在BC上,则BF长为多少时,使得ΔDCF∽ΔDAE?[参考答案]1.⑴F⑵F⑶T⑷T⑸T⑹F⑺F⑻T2.C3.12提示:ΔA″B″C″∽ΔABC,由题设条件已知=4且=3,∴=•=4×3=124.提示:∵显然ΔABD∽ΔCBE,再根据夹角相等且两边对应成比例证明即可。5.提示:∵∠A=∠C,∴只需证夹角的两边对应成比例即可