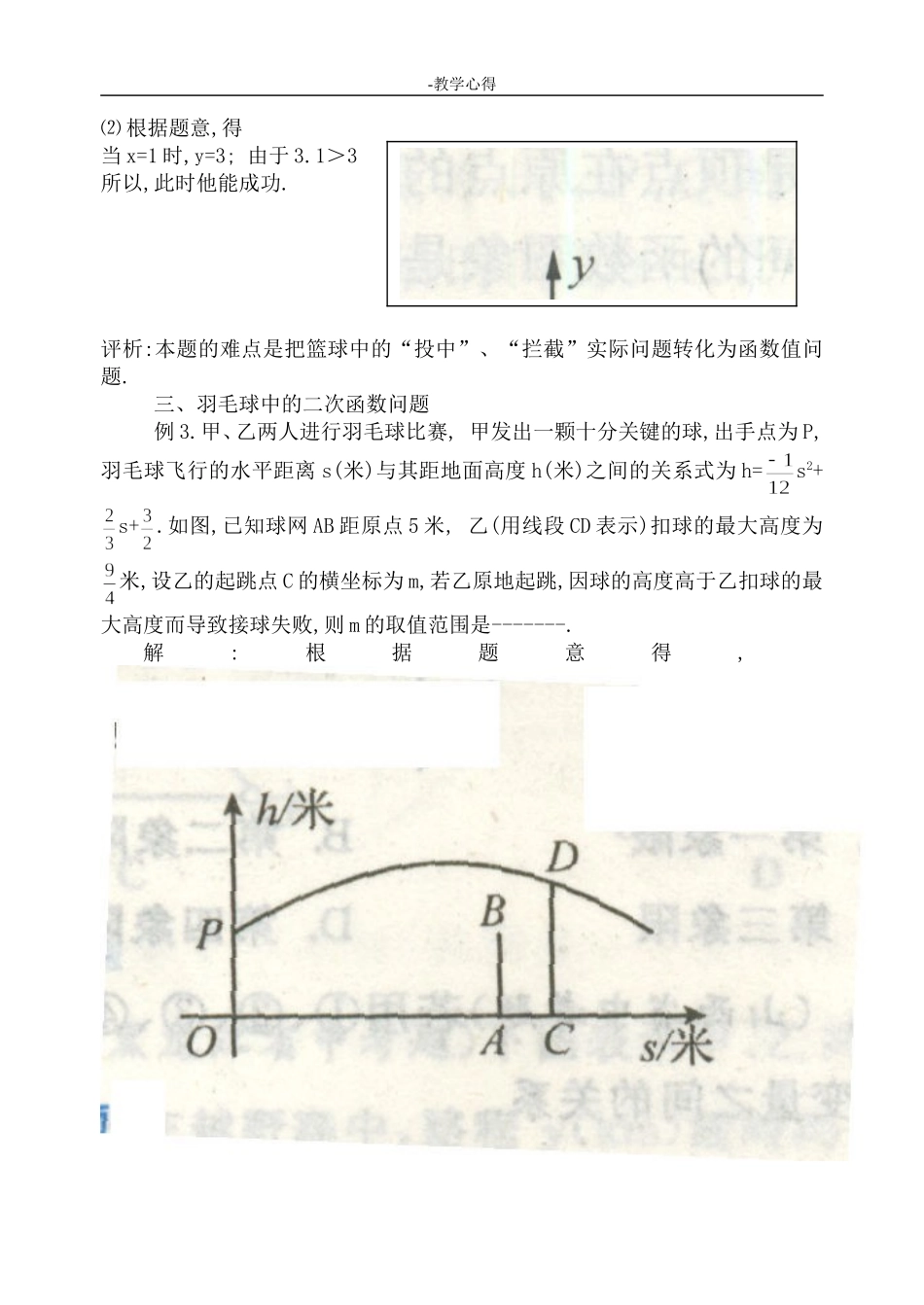
-教学心得体育活动中的二次函数朱兴华《数学课程标准》指出要让学生体会到生活中处处有数学,同时强调数学活动要从学生已有的生活经验出发,让学生亲身经历将实际问题抽象成数学模型并解释与应用的过程.下面结合具体事例探讨体育活动中的二次函数问题.一、足球中的二次函数问题例1.一场足球比赛中,某球员在离球门6m远的地方抬脚劲射,从高速摄影机拍得的资料,足球沿抛物线飞向球门,并且在如图的直角坐标系中,该抛物线对应的二次函数为y=a(x-4)2+3.2,若球门的横梁高为2.44m,此球有进门的可能吗?分析:用函数解决问题的关键在于建立适当的直角坐标系,此题以射门点为坐标轴的原点是适当的.球能否进门关键在于图象与球框交点的纵坐标的大小,要注意纵坐标此时高于球框是不能射进球门的.此题不仅考察了学生用待定系数法求二次函数解析式的问题,同时数学的建模思想也得到了很好的巩固.解:根据题意得,y=a(x-4)2+3.2经过点A(0,0),则0=16a+3.2a=-0.2∴此函数解析式为:y=-0.2(x-4)2+3.2当x=6时,y=2.4.∵2.4<2.44∴此球能进球门.评析:本题已建立了二次函数的数学模型,解题者只要根据模型进行解释与应用.二、篮球中的二次函数问题例2.某校九年级的一场篮球比赛中,如图,队员甲正在投篮,已知球出手时离地面m,与篮圈中心的水平距离为7m,当球出手后水平距离为4m时到达最大高度4m,设篮球的运行轨迹为抛物线,篮圈距地面3m.(1)建立如图所示的平面直角坐标系,问此球能否准确投中?(2)此时,若对方队员乙在甲前面1m处跳起盖帽拦截,已知乙的最大摸高为3.1m,那么他能否获得成功?分析:此题与上题同是学生关注的体育问题.它的解题关键也在于建立适当的直角坐标系,先求出二次函数的解析式,再求出相关点的坐标进行比较.此时的坐标轴可以以投篮运动员的立足点为原点.设顶点式:y=a(x-h)2+k.解:⑴根据题意,得y=a(x-4)2+4,由图象经过点(0,),得a=-∴此函数解析式为y=-(x-4)2+4;当x=7时,y=3,∴此球能进.-教学心得⑵根据题意,得当x=1时,y=3;由于3.1>3所以,此时他能成功.评析:本题的难点是把篮球中的“投中”、“拦截”实际问题转化为函数值问题.三、羽毛球中的二次函数问题例3.甲、乙两人进行羽毛球比赛,甲发出一颗十分关键的球,出手点为P,羽毛球飞行的水平距离s(米)与其距地面高度h(米)之间的关系式为h=s2+s+.如图,已知球网AB距原点5米,乙(用线段CD表示)扣球的最大高度为米,设乙的起跳点C的横坐标为m,若乙原地起跳,因球的高度高于乙扣球的最大高度而导致接球失败,则m的取值范围是-------.解:根据题意得,-教学心得当x=m时,y=m2+m+因接球失败,所以y>则,m2-8m+9<0∴4-<m<4+.∵m>5,∴5<m<4+评析:本题的关键是把“扣球”问题转化为函数值及不等式问题,可见建立了数学模型后,接下来就要把题目中的实际问题再次转化为数学中的某个或某几个具体问题.平时的学习中应认识到现实生活中蕴涵着大量的数学信息、数学在现实生活中有着广泛的应用;面对实际问题时,能主动尝试着从数学的角度运用所学知识和方法寻找解决问题的策略,这对掌握“双基”,培养思维品质、应用能力和创新意识等方面,都会起到促进作用.