223向量的数乘(1)VIP免费

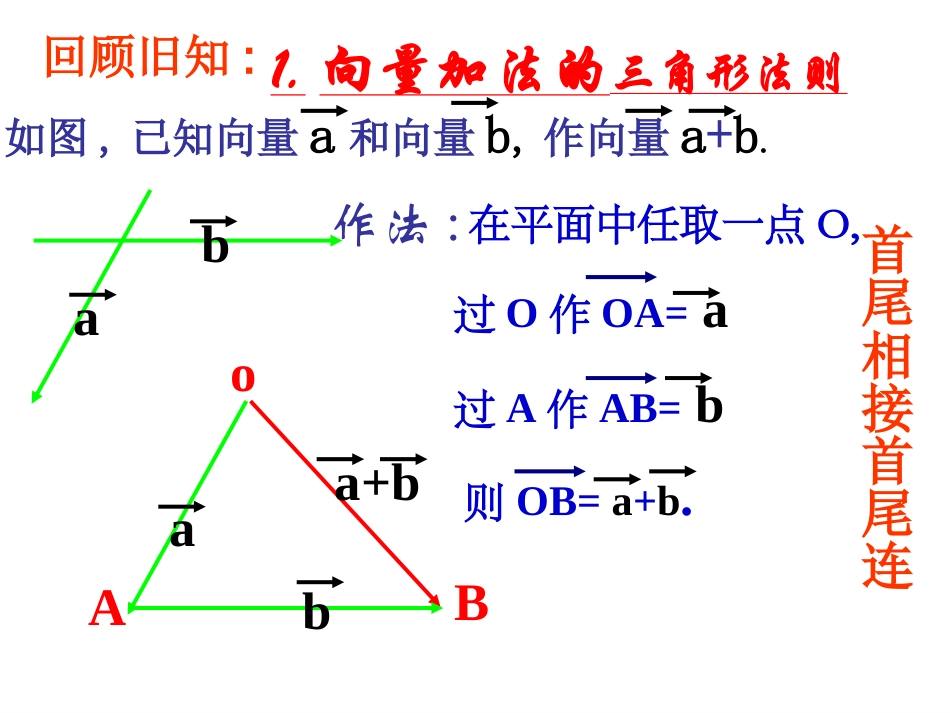
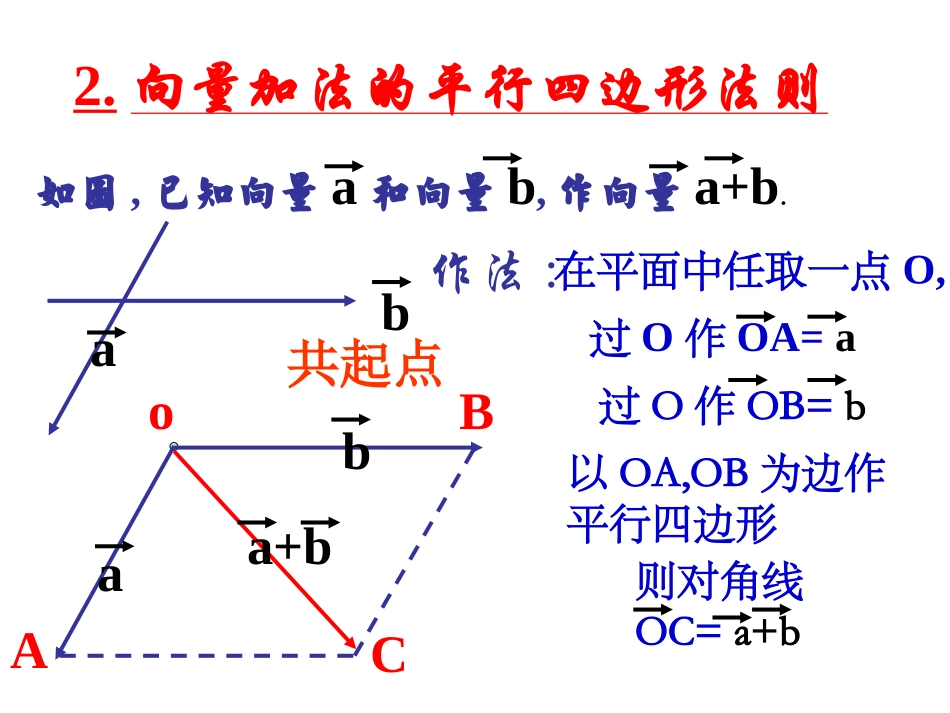
第2章平面向量2.2.3向量的数乘（1）1.向量加法的三角形法则作法:在平面中任取一点O,o回顾旧知:过O作OA=a过A作AB=b则OB=a+b.a+bbaA如图,已知向量a和向量b,作向量a+b.bBa首尾相接首尾连2.向量加法的平行四边形法则作法:在平面中任取一点O,o以OA,OB为边作平行四边形C如图,已知向量a和向量b,作向量a+b.baaAbB过O作OA=a过O作OB=ba+b则对角线OC=a+b共起点3.向量的减法(三角形法则）如图,已知向量a和向量b,作向量a-b.ab作法:在平面中任取一点O,oaAa-bbB共起点过O作OA=a过O作OB=b则BA=a-b实际背景,33一物体作匀速直线运动，一秒钟的位移对应向量那么在同方向上秒的位移对应的向量用表示，试画出该向量。aaaa3探索1:aaCCaaAABBaaOO-a-aQQ-a-aMMNN-a-aPP已知非零向量已知非零向量aa（如图）（如图）aa试作出：试作出：aa++aa++aa和和(-(-aa)+(-)+(-aa)+(-)+(-aa))根据向量加法的法则可得思考思考::相同向量相加以相同向量相加以后，后，和的长度与方向有什么变化？和的长度与方向有什么变化？3a3aOaaaABC3a由图可知，向量OC=OA+AB+BC=a+a+a,我们把a+a+a记作3a，即OC=3a.显然，3a的方向与a的方向相同，3a的长度是a的长度的3倍，即|3a|=3|a|.PQaMaNa3a由图可知，PN=PQ+QM+MN=(-a)+(-a)+(-a)，把(-a)+(-a)+(-a)记作-3a，即PN=-3a显然，-3a的方向与a的方向相反，-3a的长度是a的长度的3倍，即|-3a|=3|a|。||||||;aa（1）一般地，我们规定实数λ与向量的积是一个向量，这种运算叫做向量的数乘，记作，它的长度和方向规定如下：aa（2）当时，的方向与的方向相同；当时，的方向与的方向相反。aa0aa0特别的，当时，00.a思考:向量数乘和实数乘法有那些相同点?那些不同点?①a是一个向量；②a的长度等于的绝对值与向量a的长度的乘积。a)2(3a)2(3aa6=abbaba22a2b2baba22)(2探索2:(1)(1)根据定义，求作向量根据定义，求作向量3(23(2aa))和和(6(6aa))((aa为非零向量为非零向量))，并进行比较。，并进行比较。(2)(2)已知向量已知向量a,ba,b，求作向量，求作向量2(2(a+ba+b))和和22a+a+22bb，，并进行比较。并进行比较。设为实数，那么,���(1)λ(μa)=(λμ)a;(2)(λ+μ)a=λa+μa;(3)λ(a+b)=λa+λb.特别的，我们有��(-λ)a=-(λa)=λ(-a),λ(a-b)=λa-λb.向量的加、减、数乘运算统称为向量的线形运算.对于任意向量，以及任意实数，恒有12λ、μ、μ1111.abab=（）�a、b第一分配律第二分配律例1.计算：(3)4;3()2();(23)(32).aababaabcabc(1)(2)(3)11225352ababc解：12263)3(342);(2)3()2(2)4()0.abcabcxaxaxabx巩固练：计算：（）（已知求习cbacba612961241）原式解：（a13043044442332baxbaxaxax）（bax43例2探索.如图：已知，，试判断与是否共线．ABAD3BCDE3ACAEBCAB33BCAB3AC3ABDEC∴与共线．AEACDEADAE解：