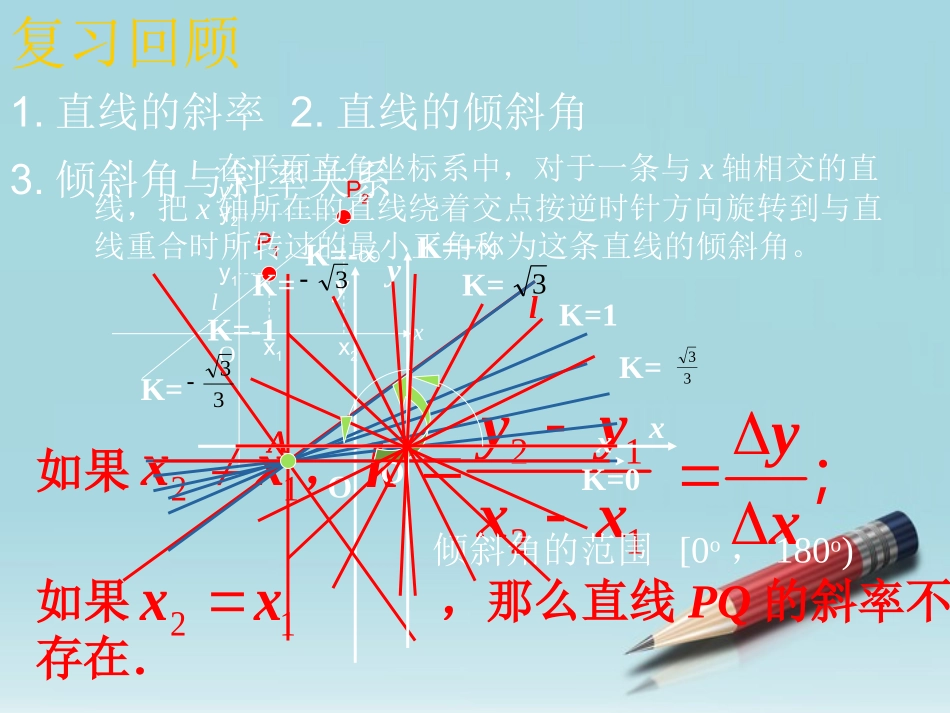
直线的方程—点斜式问题二:由一点和斜率确定的直线上的点的坐标应满足什么条件呢?问题一:如何确定一条直线?复习回顾1.直线的斜率lxyOP2P1y2x1y1x2yx;21xx2121yykxx如果,3.倾斜角与斜率关系2.直线的倾斜角如果,那么直线PQ的斜率不存在.21xxOxy在平面直角坐标系中,对于一条与x轴相交的直线,把x轴所在的直线绕着交点按逆时针方向旋转到与直线重合时所转过的最小正角称为这条直线的倾斜角。lAA倾斜角的范围[0o,180o)OxyK=0K=33K=1K=33K=+∞K=33K=-1K=K=-∞实践出真知:直线l经过点A(-1,3),斜率为-2,任一点P在l上运动,那么点P的坐标(x,y)应满足什么条件?反思:求直线的方程的实质?APPPPPPPP直线的点斜式方程:11yykxx例1.已知一条直线经过点P(-2,3),斜率为2,求这条直线方程.y-3=2(x+2)y=2x+7例2.已知直线l的斜率为k,与y轴的交点是P(0,b),求直线l的方程.y=kx+b直线的斜截式方程:y=kx+b归纳点斜式的特点:1.从方程可以看出该直线的斜率和必经过的一点;2.以斜率K存在为前提;3.当P为一特殊点时,P(0,b)直线方程为斜截式;y=kx+b,b的几何意义是:在y轴上的截距对斜截式方程的探究:探究一:截距是不是距离?是不是一定要为正?探究二:直线斜截式方程与一次函数关系?探究三:直线y=kx+2和直线y=x+b有怎样的特征?1直线kx-y-2k+1=0必经过一点为(,)2过点A(1,3)B(1,-4)的直线方程为3讨论直线y=kx+b位置:当k>0,b>0时,直线y=kx+b不经过第象限;当k>0,b<0时,直线y=kx+b不经过第象限;当k<0,b>0时,直线y=kx+b不经过第象限;当k<0,b<0时,直线y=kx+b不经过第象限;例:直线y=2x+1不经过第象限?直线y=kx+b的图象不经过第二象限,则b0,k021x=1练习1.根据下列条件,直接写出直线的方程(1)经过点(4,-2),斜率为3(2)经过点(3,1),斜率为(3)斜率为-2,在y轴上的截距为-2(4)斜率为,与x轴的交点横坐标为-71232练习2.直线y=k(x+1)(k>0)的图象可能是()A11yxoB-11yxoC-1-1yxoBD-11x练习3.(1)已知一直线经过点P(1,2),且与直线y=-2x+3斜率相等,则直线方程是.(2)已知一直线斜率为0,且在y轴上的截距为-2,则该直线方程是________.y=-2x+4y=-2任一条直线都可以用点斜式方程表示吗?斜截式方程可以改写为点斜式方程吗?已知直线l经过点P(2,1),且它的倾斜角是直线:y=x+2的一半,求直线l的方程.31l若直线点P(0,1),它与两条坐标轴围成的三角形的面积等于4,求直线的方程.若直线点P(1,1),它与两条坐标轴围成的三角形的面积等于4,求直线的方程.今天我们研究了直线方程的点斜式和斜截式,它们在使用时的优点是什么?有何限制条件?已知直线过点,且与x轴、y轴的正半轴分别交于A、B两点,(1)求△ABO的面积的最小值及其这时的直线l的方程;(2)求直线l在两坐标轴上截距之和的最小值。