高一数学一元二次不等式教学课件 必修5 0 课件VIP免费

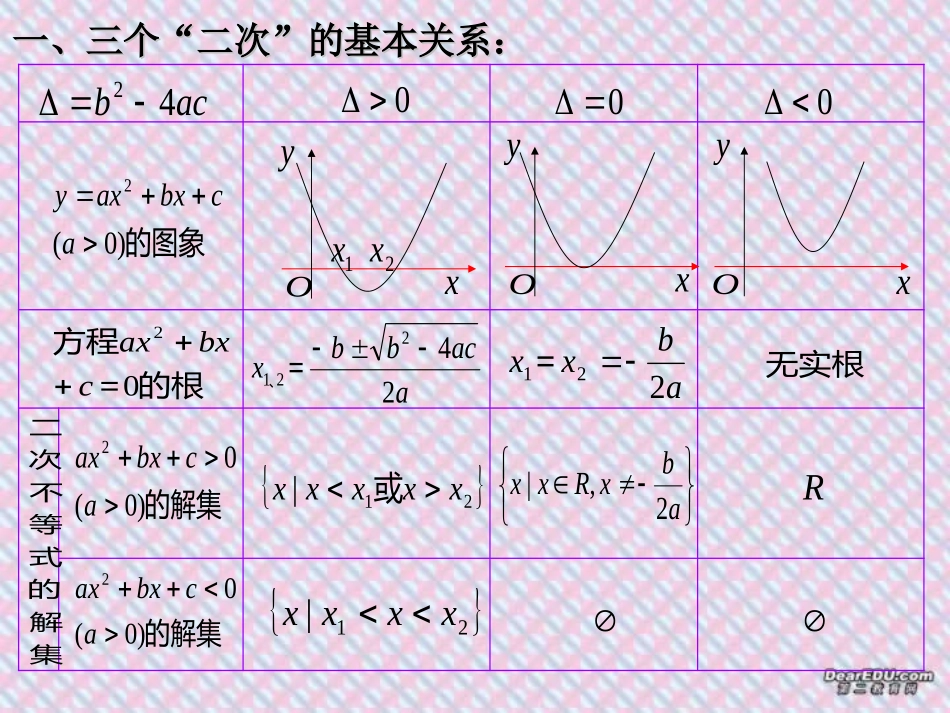
一元二次不等式一元二次不等式一、三个“二次”的基本关系：一、三个“二次”的基本关系：acb42000的图象)0(2acbxaxy的根＝方程02cbxax的解集)0(02acbxax的解集)0(02acbxaxxyOxyOxyO1x2xaacbbx24221＝、abxx221＝无实根21|xxxxx或21|xxxxabxRxx2,|R集解的式等不次二二、典型题选讲（一元二次不等式）解下列不等式026)3(0453)2(02730)1(222xxxxxx解：}625{0)6)(52(03072)1(2xxxxxxx或不等式解集为即原不等式变为。不等式解集为R,04825)2(}2132{0)12)(23()3(xxxx不等式解集为原不等式变为例1.x2+5ax+6>0解：由题意，得：⊿=25a2－241.当⊿=25a2－24>0，;22224525224525aaxaaxx或2.当⊿=25a2－24=0，3.当⊿=25a2－24<0,解集为：解集为：;25axRxx且时652652即a解集为：R.时652或652即aa时即652a二、典型题选讲（含参不等式的解法）变式1.x2+5ax+6a2>0解：因式分解，得:（x+3a)(x+2a)>0，方程（x+3a)(x+2a)＝0的两根为－3a、－2a.①当－3a>－2a即a<0时，解集为：{x︱x>－3a或x<－2a};②当－3a=－2a即a=0时，解集为：{x︱x∈R且x≠0}；③当－3a<－2a即a>0时，综上：当a>0时，解集为：{x︱x>－2a或x<－3a}.当a=0时，解集为：{x︱x∈R且x≠0};当a<0时，解集为：{x︱x>－3a或x<－2a};解集为：{x︱x>－2a或x<－3a}.原不等式为x2>0变式2.ax2+(6a+1)x+6>0二、当a≠0时，6|解集为xx①当a<0时，,01aaxx16解集为一、当a=0时，②当a>0时，01a⑴时即当616,1aa6或1:解集为xaxx⑶⑵时即当616,1aa6或:解集为xRxx时即当6106,1aaaxxx1或6:解集为6,1两根为061方程axax的∴综上，得;1x6x0.1aa时，解集为当;10.2xxa解集为时当，;1或6解集为时610当.3axxxa，;661.4xRxxa且解集为时当，.6161.5xaxxa或时，解集为当06x1x因式分解，得：a注：注：解形如解形如axax22+bx+c+bx+c>>00的不等式时分类讨的不等式时分类讨论的标准有：论的标准有：11、讨论、讨论aa与与00的大小；的大小；22、讨论、讨论⊿⊿与与00的大小；的大小；33、讨论两根的大小；、讨论两根的大小；例2关于x的二次不等式a2x2+6ax+9－b2≤0的解集是[－1，2]，求a,b解：依题意知方程a2x2+6ax+9—b2=0的两根为—1,2∴9696baba或解得：（1）二次不等式ax2+bx+c>0恒成立例题：已知关于x的不等式：(a-2)x2+(a-2)x+1≥0恒成立，解：由题意知：①当a-2=0，即a=2时，不等式化为②当a-2≠0，即a≠2时，原题等价于220(2)4(2)0aaa综上：试求a的取值范围.1≥0，它恒成立，满足条件.2(2)(6)0aaa即226aa即26a所以26a知识概要（2）二次不等式ax2+bx+c<0恒成立2040abac2040abac（3）二次不等式ax2+bx+c≥0恒成立2040abac（4）二次不等式ax2+bx+c≤0恒成立0402acba(二)含参不等式恒成立的问题三、课堂小结1、解含参数的不等式2、已知不等式的解集，求参数的值或范围不等式中的恒成立问题一、内容分析二、运用的数学思想1、分类讨论的思想3、等与不等的化归思想2、数形结合的思想用图象分离参数后用最值函数、、、321