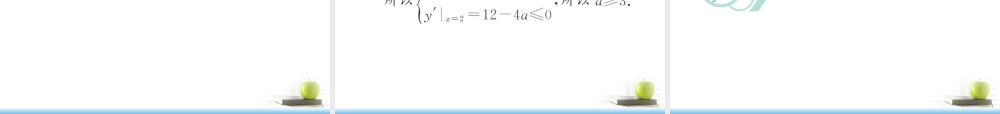掌握利用导数研究函数的单调性,求函数的极值和最值的方法. 1()0()0()()2()0 )(1 0()aby f xfxy f xabfxababf xaby f xfxfxababf x对于定义在区间 , 内连续不间断的函数 =,由=在 , 内单调递增在 , 内恒成立,其中 ,为的单调递增区间;对于定义在区.函数的单调性间 , 内连续不间断的函数 =,由① 在 , 内恒成立,其中区间 ,为的单与调其导数的关系递减区间. 00000000001_____________________22f xxxxxf xf xyf xxf xf xyf xxxf x极大值极小值极值与极值点:设函数在点 及其附近有定义,如果对 附近的异于 的所有点 ,都有②,则称为的极大值,记作=, 为极大值点.反之,若③,则称为的极小值,记作=, 为极小值点,极大值和极小值统称为极值,极大值点和极小值点统称为.函数极值点. 若 为可导函数的极值与其导数的关的极值点系,则有④ _____;反之,不一定成立. 00max00min01 ___________2[]__________[]3y f xIxxIf xyf xf xyf xy f xabab.函数的最值:如果在函数 =的定义域 内存在,使得对任意的,都有⑤,则称为函数的最大值,记作=;反之,若有⑥,则称为函数的最小值,记作=.最大值和最小值统称为最值;如果函数的最函数 =在闭区间 , 上的图象是⑦的曲线,则该函数在闭区间值与其的关系,导数上一定能够取得最大值与最小值.4()()()()()()()ab极值是反映函数的局部性质,最值是反映函数的整体性质.极大 小 值不一定是最大 小 值,最大小 值也不一定是极大 小 值,极大值不一定比极小值大.但如果函数的图象是一条不间断的曲线,在区间 , 内只有一个极值.极值与最值的区,那么极大 小 值就别与是最大系小联值. 00000()0y f xabf xf xf xf xfxf xf xf xf x【要点指① =在 , 内单调递减;②;③;④=;⑤;⑥;⑦一条南】连续不间断 1.函数 f(x)=x+9x的单调减区间为( ) A.(-3,0) B.(0,3) C.(-3,0)∪(0,3) D.(-3,0)和(0,3) 【解析】f ′(x)=1-9x2=x2-9x2 , 令 f ′(x)<0,解得-3