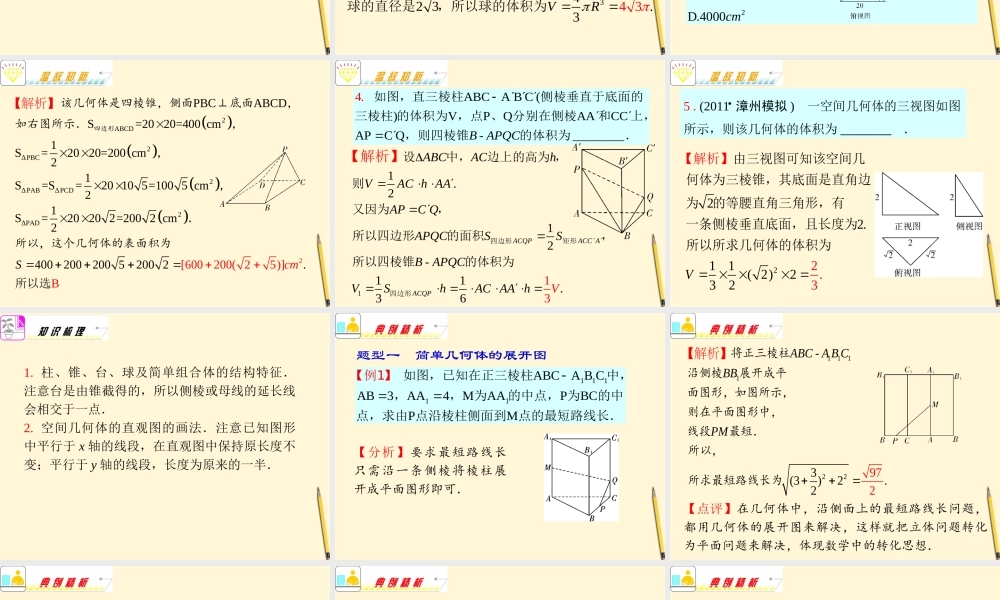
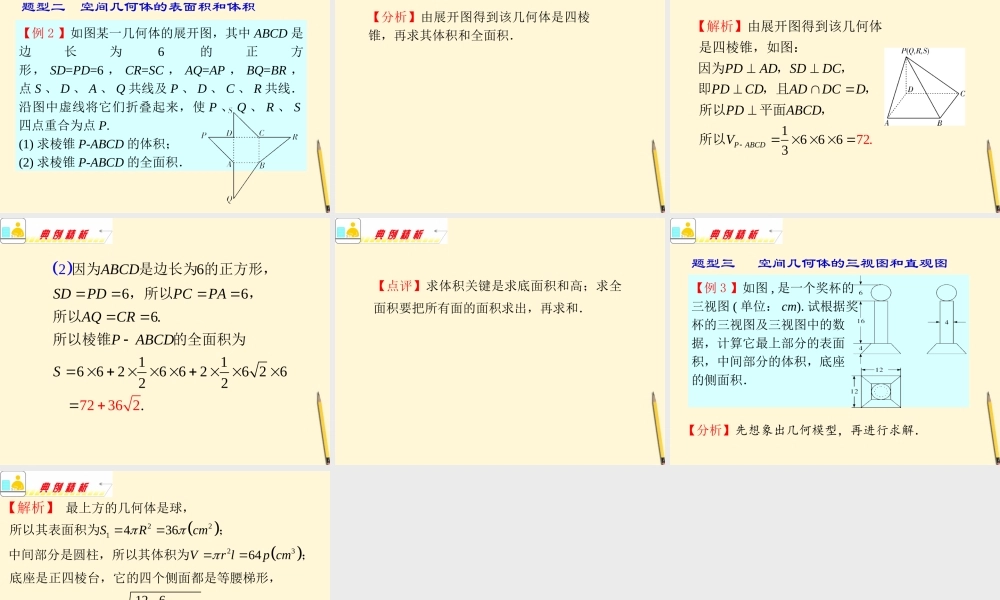
专题一 函数与导数专题五 立体几何1 .高考考点(1) 认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构;(2) 能画出简单空间图形 ( 长方体、球、圆柱、圆锥、棱柱等的简易组合 ) 的三视图,能识别上述的三视图所表示的立体模型,会用斜二测画法画出它们的直观图;(3) 了解球、棱柱、棱锥、台的表面积和体积的计算公式 ( 不要求记忆公式 ) .2 .易错易漏(1) 不能从三视图中想象出立体模型,读取相关信息;(2) 柱、锥、台的概念混乱;(3) 在斜二测画法画出的直观图中,与 y 轴平行的线段长没有取半.3 .归纳总结(1) 正确用好公式进行计算;(2) 注意从三视图中想象出立体模型,读取相关信息;(3) 解题中要贯穿转化与化归 ( 把空间问题转化为平面问题来处理 ) 、数形结合的思想.1. .(2011)()ht如图所示是某一容器的三视图,现向容器中匀速注水,容器中水面的高度 随时间 变化的图象可能是州质检 漳Bh由三视图可知该空间几何体为圆锥,刚开始单位时间内高度 变大的速度较快,随后逐渐变慢.答案:【解析】2()A.4 3 B.32 3 9 3C. 2. D.124 棱长为 的正方体的各个顶点都在同一个球上,则这个球的体积是 342 3.34 3VR【解析】易得正方体的体对角线即为球的直径,故该球的直径是,所以球的体积为2222()()A. [600 100( 52 2)] B. [600200( 52)]C.8000D.43. 000cmcmcmcmcm已知某个几何体的三视图如下,根据图中标出的尺寸 单位:,可得这个几何体的表面积是 2ABCD2ΔPBC2ΔPABΔPCD2ΔPAD2PBCABCDS=20 20=400 cm1S=20 20=200 cm21S=S=20 10 5=100 5 cm21S=20 20 2=200 2 cm24002[600200( 2500200 520)]B0 2.cSm所以选四边形该几何体是四棱锥,侧面⊥底面,如右图所示.,,,.所以,这个几何体的表面积为【解析】11.212-11361 .3ACQPACC AACQPABCAChVAC h AAAPC QAPQCSSB APQCVShCA hVAA 【解析】矩形四边形四边形设中,边上的高为 ,则又因为,所以四边形的面积,所以四棱锥的体积为 ABCA B C ()VPQAACCAPC Q-___4__.___B APQC 如图,直三棱柱侧棱垂直于底面的三棱柱 的体积为 ,点 、 分别在侧棱和上,,则四棱锥的体积为.5 . (2011 漳州模拟 ) 一空间几何体的三...