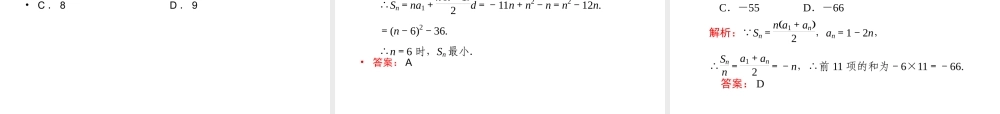•重点难点•重点:等差数列的定义、通项、前 n 项的和与性质.•难点:等差数列性质的应用. •知识归纳•一、等差数列的概念•1 .定义:如果一个数列从第二项起,每一项与它的前一项的差都等于同一个常数,这样的数列叫做等差数列.•2 .等差中项:如果三数 a 、 A 、 b 成等差数列,则 A 叫做a 和 b 的等差中项,即 A =•. •二、等差数列的通项公式•对于等差数列 {an} ,则 an= a1+d = am+d.•推导方法:累加法 an= (an- an - 1) + (an - 1- an - 2) +…+ (a2- a1) + a1.•三、等差数列的前 n 项和公式•Sn ==.•推导方法:倒序相加法.(n - 1)(n - m) •四、用函数观点认识等差数列•1 . an= nd + (a1- d)( 一次函数 ) .•2 . Sn= n2+ (a1- )n( 常数项为零的二次函数 ) .•五、等差数列的判定方法•(1) 定义法: an + 1- an= d( 常数 )(n∈N*){⇔ an} 是等差数列;•(2) 中项公式法: 2an + 1= an+ an + 2(n∈N*){⇔ an} 是等差数列;•(3) 通项公式法: an= kn + b(k , b 是常数 )(n∈N*){⇔ an}是等差数列; •(4) 前 n 项和公式法: Sn= An2+ Bn(A 、 B 是常数 )(n∈N*)⇔{an} 是等差数列.(5){an}是等差数列⇔ {Snn }是等差数列. •六、等差数列的性质•1 .下标和与项的和的关系•在等差数列中,若 p + q = m + n ,则有 ap+ aq= am+ an;若 2m = p + q ,则有 ap+ aq= , (p , q ,m , n∈N*) .2am2.任意两项的关系 在等差数列{an}中,m、n∈N*,则 am-an=(m-n)d或 am=an+(m-n)d 或am-anm-n =d. •3 .在等差数列中,等距离取出若干项也构成一个等差列,即 an, an + m, an + 2m…,为等差数列,公差为 md.•等差数列的依次 n 项和也构成一个等差数列,即 Sn, S2n-Sn, S3n- S2n……,为等差数列,公差为 n2d.•即下标成等差的项成等差数列,下标和成等差的具有相同构成规律的项的和成等差数列. 4.设等差数列{an}的公差为 d,那么 (1)d>0⇔ {an}是递增数列,Sn 有最小值;d<0⇔ {an}是递减数列,Sn 有最大值;d=0⇔ {an}是常数数列. (2)数列{λan+b}仍为等差数列,公差为 λd. (3)若{bn},{an}都是等差数列,则{an±bn}仍为等差数列. (4)项数为 n 的等差数列...