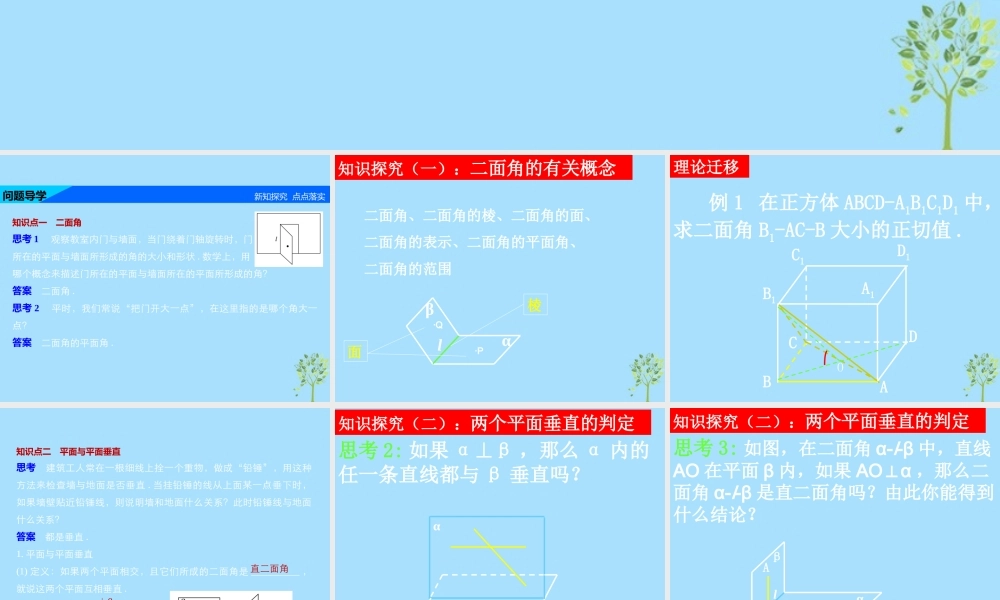
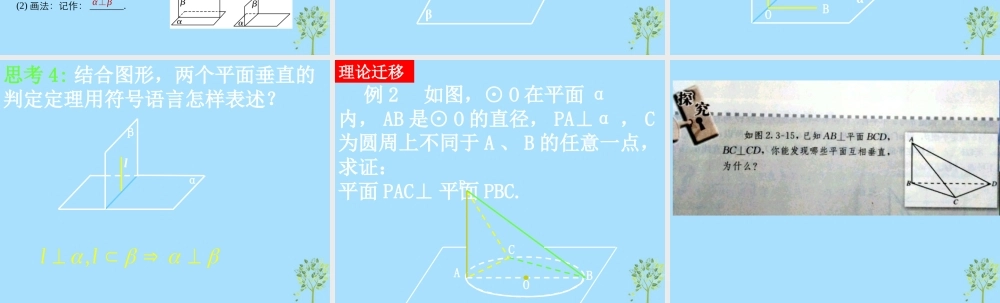
平面与平面垂直平面与平面垂直问题导学 新知探究 点点落实知识点一 二面角思考 1 观察教室内门与墙面,当门绕着门轴旋转时,门所在的平面与墙面所形成的角的大小和形状 . 数学上,用哪个概念来描述门所在的平面与墙面所在的平面所形成的角?答案 二面角 .思考 2 平时,我们常说“把门开大一点”,在这里指的是哪个角大一点?答案 二面角的平面角 .二面角、二面角的棱、二面角的面、二面角的表示、二面角的平面角、二面角的范围lαβ棱面·P·Q知识探究(一):二面角的有关概念 理论迁移 例 1 在正方体 ABCD-A1B1C1D1 中,求二面角 B1-AC-B 大小的正切值 .AA1BCDB1C1D1O知识点二 平面与平面垂直思考 建筑工人常在一根细线上拴一个重物,做成“铅锤”,用这种方法来检查墙与地面是否垂直 . 当挂铅锤的线从上面某一点垂下时,如果墙壁贴近铅锤线,则说明墙和地面什么关系?此时铅锤线与地面什么关系?答案 都是垂直 .1. 平面与平面垂直(1) 定义:如果两个平面相交,且它们所成的二面角是 __________ ,就说这两个平面互相垂直 .(2) 画法:记作: _______.直二面角α⊥βαβ思考 2: 如果 α⊥β ,那么 α 内的任一条直线都与 β 垂直吗?知识探究(二):两个平面垂直的判定 知识探究(二):两个平面垂直的判定 思考 3: 如图,在二面角 α-l-β 中,直线AO 在平面 β 内,如果 AOα⊥,那么二面角 α-l-β 是直二面角吗?由此你能得到什么结论?αβABOl思考 4: 结合图形,两个平面垂直的判定定理用符号语言怎样表述?αβl,ll理论迁移 例 2 如图,⊙ O 在平面 α内, AB 是⊙ O 的直径, PA⊥α , C为圆周上不同于 A 、 B 的任意一点,求证:平面 PAC⊥ 平面 PBC. PABCO