山西省忻州市高考数学 专题 类比复习课件VIP免费

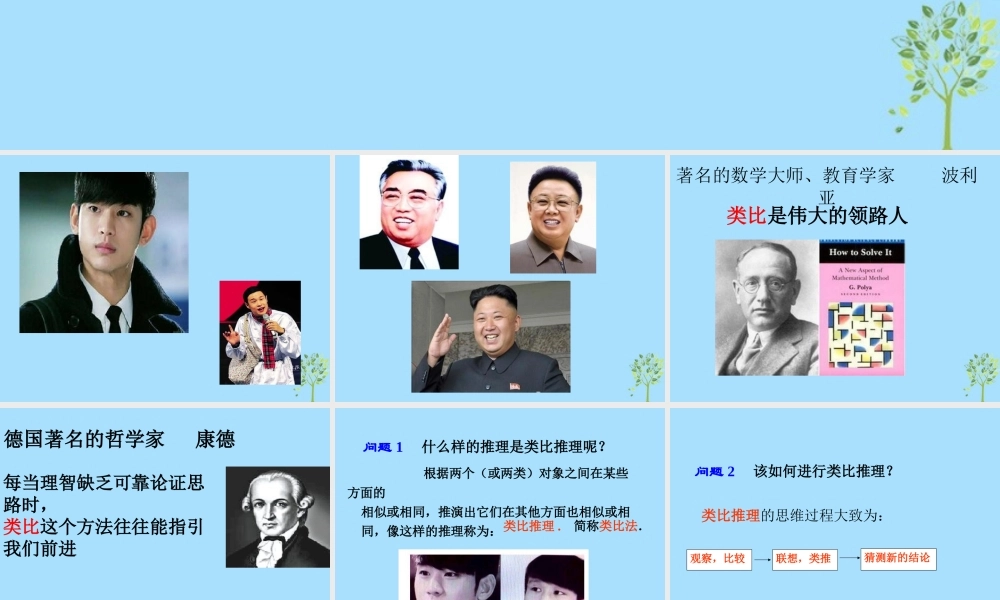
著名的数学大师、教育学家 波利亚类比是伟大的领路人德国著名的哲学家 康德每当理智缺乏可靠论证思路时，类比这个方法往往能指引我们前进 根据两个（或两类）对象之间在某些方面的相似或相同，推演出它们在其他方面也相似或相同，像这样的推理称为：类比推理 .简称类比法．问题 1 什么样的推理是类比推理呢？问题 2 该如何进行类比推理？类比推理的思维过程大致为：观察，比较联想，类推猜测新的结论类比推理的一般模式为： A 类事物具有性质 a,b,c,d; B 类事物具有性质 a′,b′,c′; A 类事物具有性质 d, 所以，B 类事物可能具有性质 d′. a, b,c 与 a′,b′,c′相似或相同， 例：（G.波利亚的类比）类比实数的加法与乘法，并列出它们类似的性质。 加法的性质 乘法的性质 a+b=b+a ab=ba (ab)c=a(bc) a+(-a)=0 a×1=a 加法的性质 乘法的性质 a+b=b+a ab=ba (ab)c=a(bc) a+(-a)=0 a×1=a ()()abcabc 1()1aa0aa变式：关于平面向量的数量积运算与实数的乘法运算相类比，可得到哪些结论： ①abba；②)()(cbacba； ③cabacba)(；④baba； ⑤由caba,可得cb ． 问题 3 类比推理的结论一定成立吗？（ 1 ）（ 3 ）通过类比得到的结论正确的有 _________.变式：关于平面向量的数量积运算与实数的乘法运算相类比，可得到哪些结论： 等差数列 等比数列 定 义 通 项 公 式 12)nnaadn（12)（nnaq na11()nnaa qnN1(1)()naandnN()( ,)nmaanm dn mN( ,)n mnmaa qn mN回顾等差数列、等比数列的定义、通项 等差数列 等比数列 性质 1 性质 2 ,( , , ,)mnpqmnpqaaaam n p qN  若则,( , , ,)mnpqmnpqaaaam n p qN  若则2 ,2( , ,)mnpmnpaaam n pN 若则22 ,( , ,)mnpmnpaaam n pN 若则回顾等差数列、等比数列的相似之处互变规律• 加法 → 乘法• 倍乘 → 乘方• 减法 → 除法• 除法 → 开方 等差数列 等比数列 思 考 11()2(1)2()nnn aaSn nnadnN 11(1)(1) (1)1()nnnaqSaqqqnN 例 2：若等差数列的首项为 a1，公差为 d，前 n 项的和为 Sn，则数列{an}为等差数...