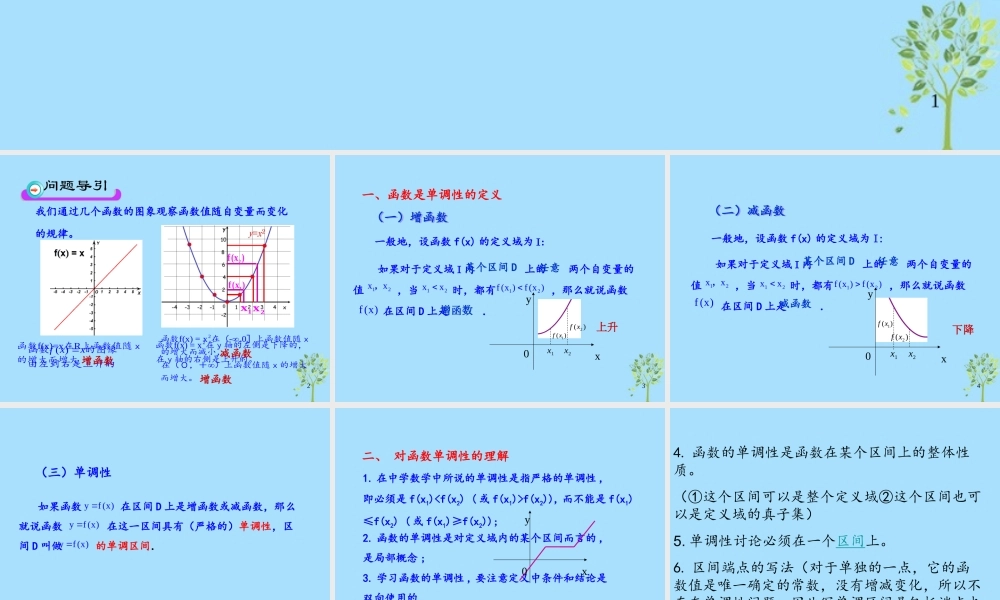
1函数的单调性 2我们通过几个函数的图象观察函数值随自变量而变化的规律。( ) f xx函数的图像由左到右是上升的2f(x) = x函数在y轴的左侧是下降的,在y轴的右侧是上升的。f(x)=xR函数在 上函数值随x的增大而增大2f(x) = x-0函数在(,]上函数值随x的增大而减小,在(0,+ )上函数值随x的增大而增大。增函数增函数减函数1x1f(x )2x2f(x )3一般地,设函数 f(x) 的定义域为 I: 一、函数是单调性的定义f (x)12xx,12xx12f (x )f (x ) 如果对于定义域 I 内 上的 两个自变量的值 ,当 时,都有 ,那么就说函数 在区间 D 上是 .某个区间 D任意增函数(一)增函数(一)增函数1x2xx0y)(1xf)(2xf上升4一般地,设函数 f(x) 的定义域为 I:f (x)12xx,12xx12f (x )f (x ) 如果对于定义域 I 内 上的 两个自变量的值 ,当 时,都有 ,那么就说函数 在区间 D 上是 .某个区间 D任意减函数(二)减函数(二)减函数x0y1x2x)( 1xf)(2xf下降5 (三)单调性 如果函数 在区间 D 上是增函数或减函数,那么就说函数 在这一区间具有(严格的)单调性,区间 D 叫做 的单调区间.yf (x)yf (x)yf (x)61. 在中学数学中所说的单调性是指严格的单调性 ,即必须是 f(x1)f(x2)), 而不能是 f(x1)≤f(x2) ( 或 f(x1)≥f(x2));二、 对函数单调性的理解2. 函数的单调性是对定义域内的某个区间而言的 ,是局部概念 ;3. 学习函数的单调性 , 要注意定义中条件和结论是双向使用的 .xy074. 函数的单调性是函数在某个区间上的整体性质。(①这个区间可以是整个定义域②这个区间也可以是定义域的真子集)5. 单调性讨论必须在一个区间上。6. 区间端点的写法(对于单独的一点,它的函数值是唯一确定的常数,没有增减变化,所以不存在单调性问题,因此写单调区间是包括端点也可以不包括也可以,但对于某些点无意义时单调区间就不包括这些点) ( 如 y= y=1 / x )12 x87. 并不是所有函数都具有单调性,有的函数不具有单调性8. 函数单调性定义中的, , 必须满足任意性,不可以随意取两个特殊值。函数单调性的几何意义:单调增函数:在定义区间上图像从左到右上升单调减区间:在定义区间上图像从左到右下降1x2x))2,1,0(,2(如xxyy9 2 、如果对于区间( a , b )上的任意 x 有 f(x) > f(a) ,则函数f(x) 在区间( a...