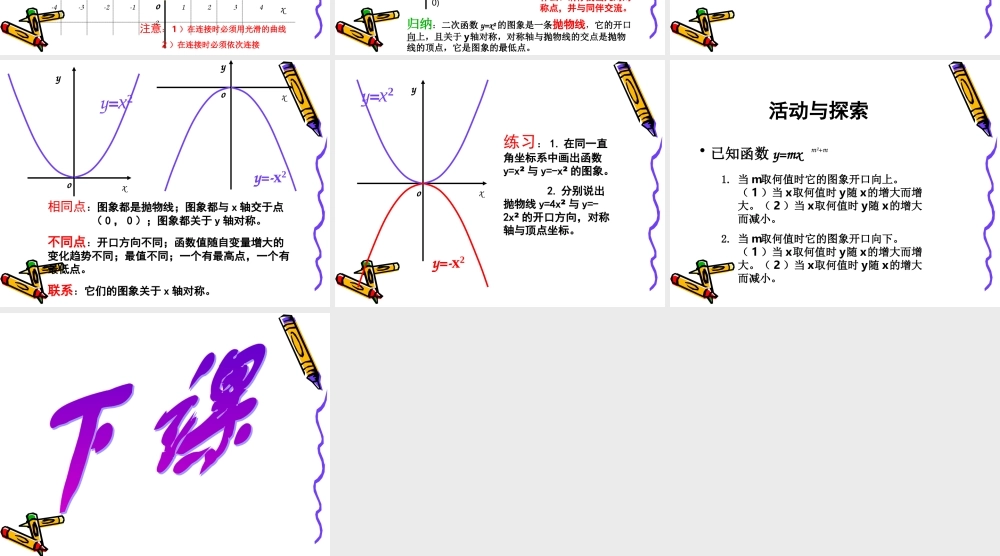
引入• 学习了正比例函数,一次函数与反比例函数的定义后,研究了它们各自的图象特征,下面请同学们谈谈它们的图象有哪些特征?• 上节课我们学习了二次函数的一般形式上节课我们学习了二次函数的一般形式为为 y=ax²+bx+cy=ax²+bx+c (( a ≠ 0a ≠ 0 ),),那么它的图象那么它的图象是否也为直线或为双曲线呢?是否也为直线或为双曲线呢? • 在二次函数 y=x2中, y随 x的变化而变化的规律是什么?• 你想直观地了解它的性质吗 ? 作二次函数 y=x2 的图象 (1) 列表 观察 y=x2的表达式,选择适当 x值,并计算相应的 y值,完成下表:x y=x2 -39-24-1100112439………… • (2) 在直角坐标系中描点连线 xyo-4-3-2-11234108642-2y=x2注意: 1 )在连接时必须用光滑的曲线 2 )在连接时必须依次连接 (-2,4)(-3,9)(-1,1)(2.4)(1,1)(3,9)yxy=x2o(0,0)1. 你能描述图象的形状吗?与同伴交流。2. 图象与 x 轴有交点吗?如果有,交点的坐标是什么?3. 当 x<0 时, y 随着 x 的增大, y 的值如何变化?当 x>0 时呢?4. 当 x 取什么值时, y 的值最小?5. 图象是轴对称图形吗?如果是,它的对称轴是什么?请你找出几对对称点,并与同伴交流。归纳:二次函数 y=x² 的图象是一条抛物线,它的开口向上,且关于 y轴对称,对称轴与抛物线的交点是抛物线的顶点,它是图象的最低点。 • 二次函数 y=-x2的图象是什么形状?• 先想一想,然后作出它的图象.• 它与二次函数 y=x2的图象有什么关系? yxxy=x2y=-x2yoo相同点:图象都是抛物线;图象都与 x 轴交于点 ( 0 , 0 );图象都关于 y 轴对称。不同点:开口方向不同;函数值随自变量增大的变化趋势不同;最值不同;一个有最高点,一个有最低点。联系:它们的图象关于 x 轴对称。 y=x2y=-x2yxo练习: 1. 在同一直角坐标系中画出函数y=x² 与 y=-x² 的图象。 2. 分别说出抛物线 y=4x² 与 y=-2x² 的开口方向,对称轴与顶点坐标。 活动与探索• 已知函数 y=mxm²+m1. 当 m取何值时它的图象开口向上。 ( 1 )当 x取何值时 y随 x的增大而增大。( 2 )当 x取何值时 y随 x的增大而减小。2. 当 m取何值时它的图象开口向下。 ( 1 )当 x取何值时 y随 x的增大而增大。( 2 )当 x取何值时 y随 x的增大而减小。