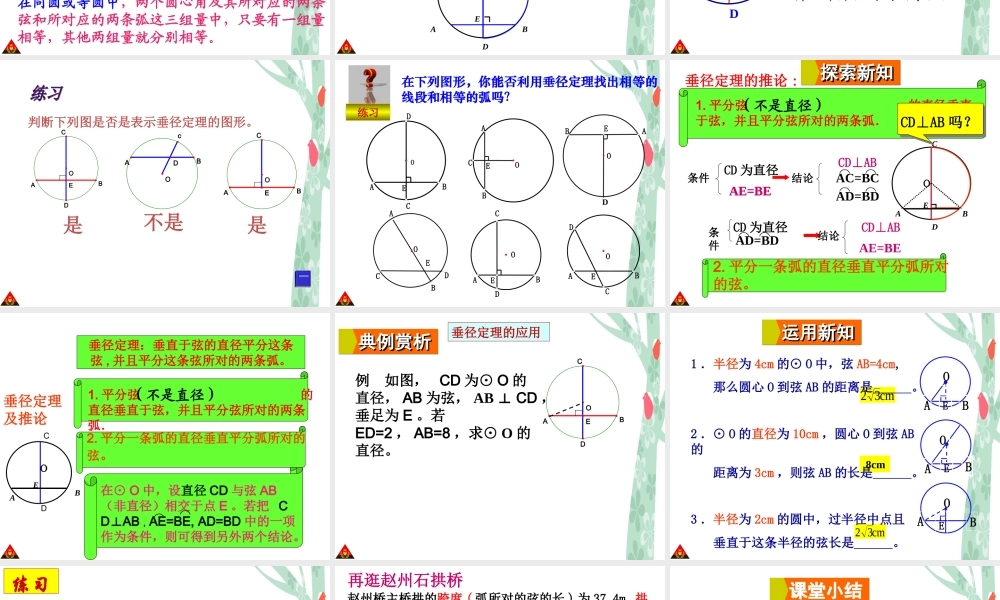
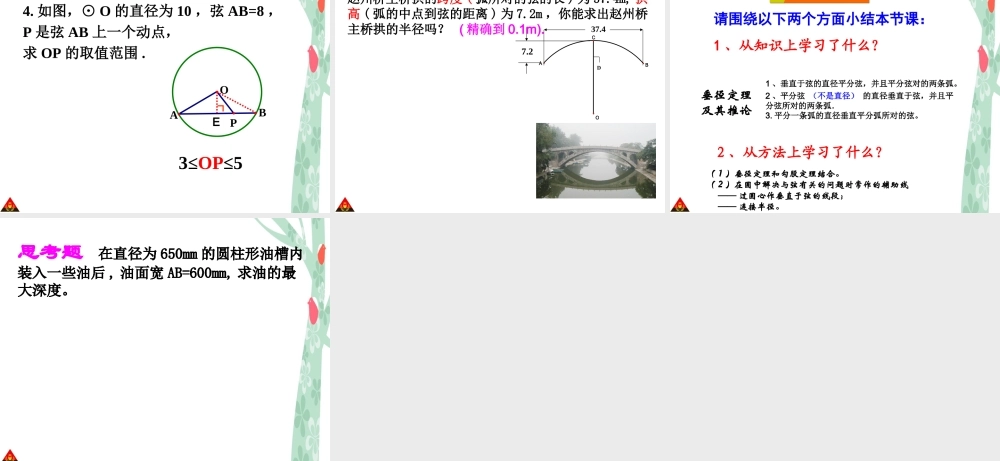
1. 理解圆是轴对称图形 , 由圆的折叠猜想垂径定理 , 并进行推理验证 .2. 理解垂径定理 , 灵活运用定理进行证明及计算 .【教学重点】垂径定理及运用 .【教学难点】用垂径定理解决实际问题 .28.4 垂径定理第 28 章 圆姜各庄初中 刘金海它是 1300 多年前我国隋朝建造的石拱桥,在河北省赵县境内,是我国古代人民勤劳与智慧的结晶。赵州桥问题情境:你知道赵州桥主桥拱的半径是多少吗?( 如图 ) 赵州桥的主桥是圆弧形 , 它的跨度 ( 弧所对的弦的长 ) 为 37.4m, 拱高 ( 弧的中点到弦的距离 , 也叫弓形高 )为 7.2m, 你能求出赵州桥主桥拱的半径吗? ( 精确到 0.1m).BACD1 、我们知道,圆是轴对称图形,那么圆的对称轴是什么?圆是轴对称图形,任何一条直径所在直线都是它的对称轴. 新课导入新课导入新课导入新课导入2 、我们前面学习了圆心角、弦和弧之间的关系,它们的关系是什么?在同圆或等圆中,两个圆心角及其所对应的两条弦和所对应的两条弧这三组量中,只要有一组量相等,其他两组量就分别相等。如图, AB 是⊙ O 的一条弦,作直径 CD ,使 CD⊥AB ,垂足为 E .( 1 )这个图形是轴对称图形吗?如果是,它的对称轴是什么?OABCDE( 2 )你能发现图中有哪些相等的线段和弧? ( 半径,半圆除外)探索新知探索新知探索新知探索新知CAEBO.D垂直于弦的直径平分弦,并且平分弦对的两条弧。CD 为⊙ O 的直径CDAB ⊥条件归纳总结归纳总结归纳总结归纳总结结论 ⌒AC=BCAC=BCAE=BEAE=BEAD=BDAD=BD ⌒ ⌒ ⌒AC=BCAC=BCAE=BEAE=BEAD=BDAD=BD ⌒AC=BCAC=BCAE=BEAE=BEAD=BDAD=BD ⌒AC=BCAC=BCAE=BEAE=BEAD=BDAD=BD ⌒AC=BCAC=BCAE=BEAE=BEAD=BDAD=BD ⌒AC=BCAC=BCAE=BEAE=BEAD=BDAD=BD ⌒AC=BCAC=BCAE=BEAE=BEAD=BDAD=BDAC=BCAC=BCAE=BEAE=BEAD=BDAD=BDAC=BCAC=BCAE=BEAE=BEAD=BDAD=BDAC=BCAC=BCAE=BEAE=BEAD=BDAD=BDAC=BCAC=BCAE=BEAE=BEAD=BDAD=BD垂径定理:EDCOAB判断下列图是否是表示垂径定理的图形。ECOABDOABc是不是是EOABDCEABCDEOABDCEOABCEOCDAB 练习OBAED在下列图形,你能否利用垂径定理找出相等的线段和相等的弧吗?OAE=BE1. 平分弦 的直径垂直于弦,并且平分弦所对的两条弧.(不是直径)CDABEO垂径定理的推论 :CD⊥AB 吗?AD=BD条件CD 为直径⌒⌒结论 CD⊥ABAE=BE2. 平分一条弧的直径垂直平分弧所对的弦。AE=BEAE=BEAC=BC⌒⌒AD=BD⌒⌒CD⊥ABAE=BE结论 条件C...