山西省忻州市高考数学 专题 空间向量复习课件VIP免费

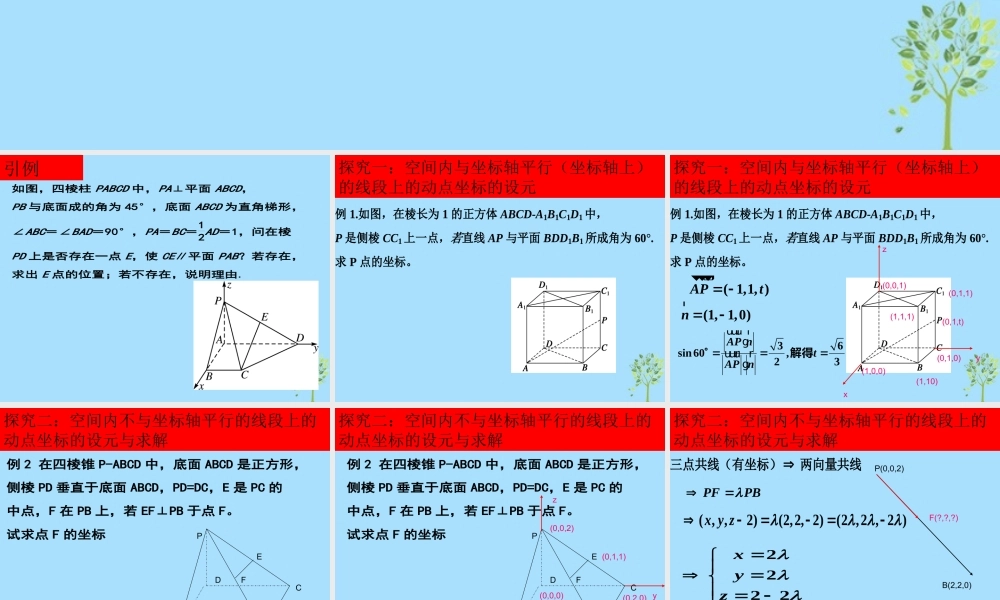
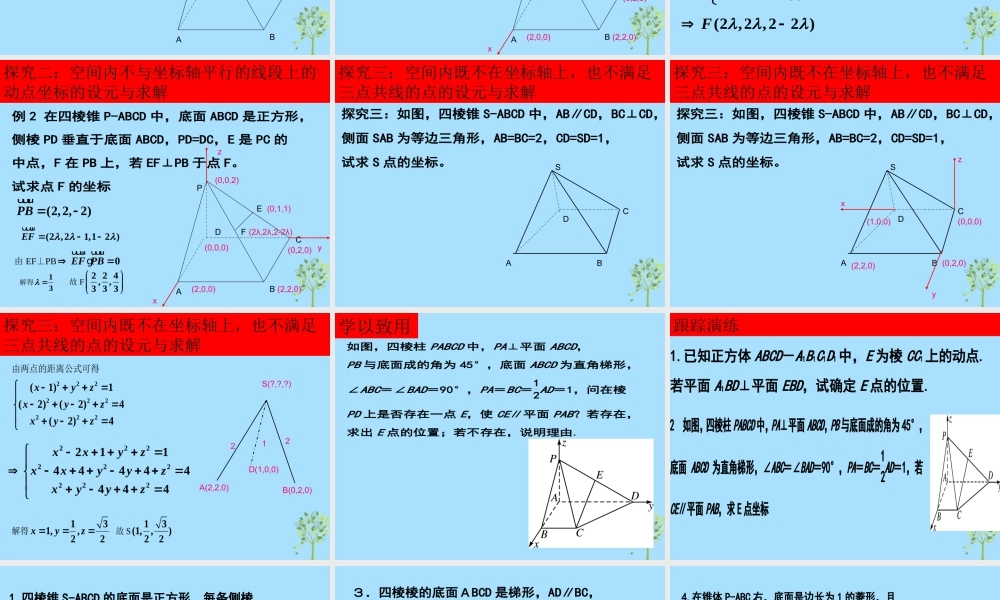
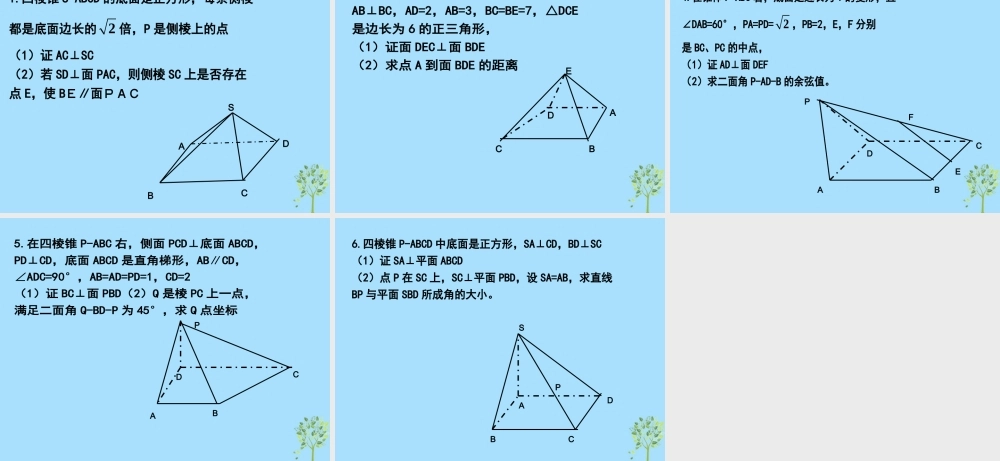
空间向量空间向量如图，四棱柱 PABCD 中，PA⊥平面 ABCD， PB 与底面成的角为 45°，底面 ABCD 为直角梯形， ∠ABC＝∠BAD＝90°，PA＝BC＝12AD＝1，问在棱 PD 上是否存在一点 E，使 CE∥平面 PAB？若存在， 求出 E 点的位置；若不存在，说明理由. 引例探究一：空间内与坐标轴平行（坐标轴上）的线段上的动点坐标的设元例 1.如图，在棱长为 1 的正方体 ABCD-A1B1C1D1 中， P 是侧棱 CC1 上一点，若直线 AP 与平面 BDD1B1 所成角为 60°. 求 P 点的坐标。 探究一：空间内与坐标轴平行（坐标轴上）的线段上的动点坐标的设元例 1.如图，在棱长为 1 的正方体 ABCD-A1B1C1D1 中， P 是侧棱 CC1 上一点，若直线 AP 与平面 BDD1B1 所成角为 60°. 求 P 点的坐标。 xyz(0,1,0)(0,1,1)(0,1,t)(1,0,0)(1,10)(0,0,1)(1,1,1)( 1,1, )APt (1, 1,0)n r36sin60,23AP ntAP n uuur rguuurrg解得探究二：空间内不与坐标轴平行的线段上的动点坐标的设元与求解PDABCEF例 2 在四棱锥 P-ABCD 中，底面 ABCD 是正方形， 侧棱 PD 垂直于底面 ABCD，PD=DC，E 是 PC 的 中点，F 在 PB 上，若 EF⊥PB 于点 F。 试求点 F 的坐标 探究二：空间内不与坐标轴平行的线段上的动点坐标的设元与求解PDABCEF例 2 在四棱锥 P-ABCD 中，底面 ABCD 是正方形， 侧棱 PD 垂直于底面 ABCD，PD=DC，E 是 PC 的 中点，F 在 PB 上，若 EF⊥PB 于点 F。 试求点 F 的坐标 xyz(0,1,1)(0,2,0)(2,2,0)(2,0,0)(0,0,2)(0,0,0)P(0,0,2)B(2,2,0)F(?,?,?)三点共线（有坐标） 两向量共线 PFPB ( , ,2)(2,2, 2)(2 ,2 , 2 )x y z 2222xyz (2 ,2 ,22 )F探究二：空间内不与坐标轴平行的线段上的动点坐标的设元与求解探究二：空间内不与坐标轴平行的线段上的动点坐标的设元与求解PDABCEF例 2 在四棱锥 P-ABCD 中，底面 ABCD 是正方形， 侧棱 PD 垂直于底面 ABCD，PD=DC，E 是 PC 的 中点，F 在 PB 上，若 EF⊥PB 于点 F。 试求点 F 的坐标 xyz(0,1,1)(0,2,0)(2,2,0)(2,0,0)(0,0,2)(0,0,0)(2λ,2λ,2-2λ)(2,2, 2)PB uuur(2 ,21,12 )EFuuur由 EF⊥PB0EF PBuuur uuurg 解得13  故 F 2 2 4,,3 3 3 探究...