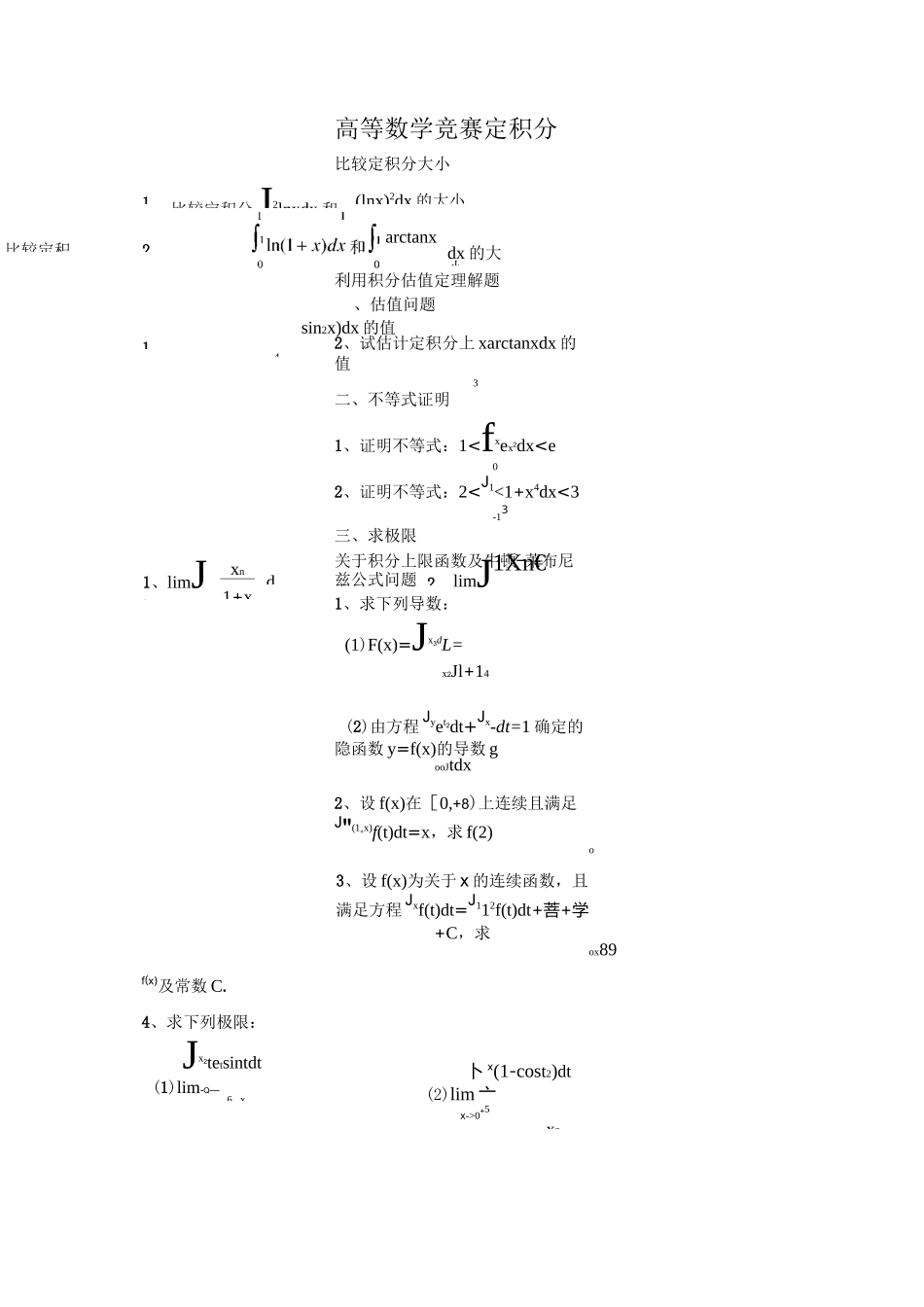
d1arctan(3)J^dx4cos2x—sinx,dxcosx(1+cosxesinx)5)lnx+2Tdxxlnx(1+xln2x)二、利用第二换元积分法求不定积分1、三角代换求下列积分xdxx3dx(1)J.(2)J-(x2+DAx2(1+x2)212、倒代换(即令 x=-)求下列积分xd1)d(a>0)x2\a2+x2dxx(x7+2)2xdx1+2x+4x1) J(x2+1)e2xdx(3)Jx2arccosxdx(4)Jx3(lnx)2dx高等数学竞赛不定积分不定积分的概念与性质1、设 f'(sin2x)=cos2x+tan2x(01f(x)及常数 C.4、求下列极限:Jx2tetsintdt(1)lim-Q—x->ox6ex卜 x(1-cost2)dt(2)lim 亠x->0+5x21、 比较定积分J2lnxdx 和(lnx)2dx 的大小2、1、sin2x)dx 的值41、limJ1xn1+xd2limJ1Xn€xdx高等数学竞赛定积分比较定积分大小利用积分估值定理解题、估值问题2、试估计定积分上 xarctanxdx 的值3二、不等式证明1、证明不等式:1