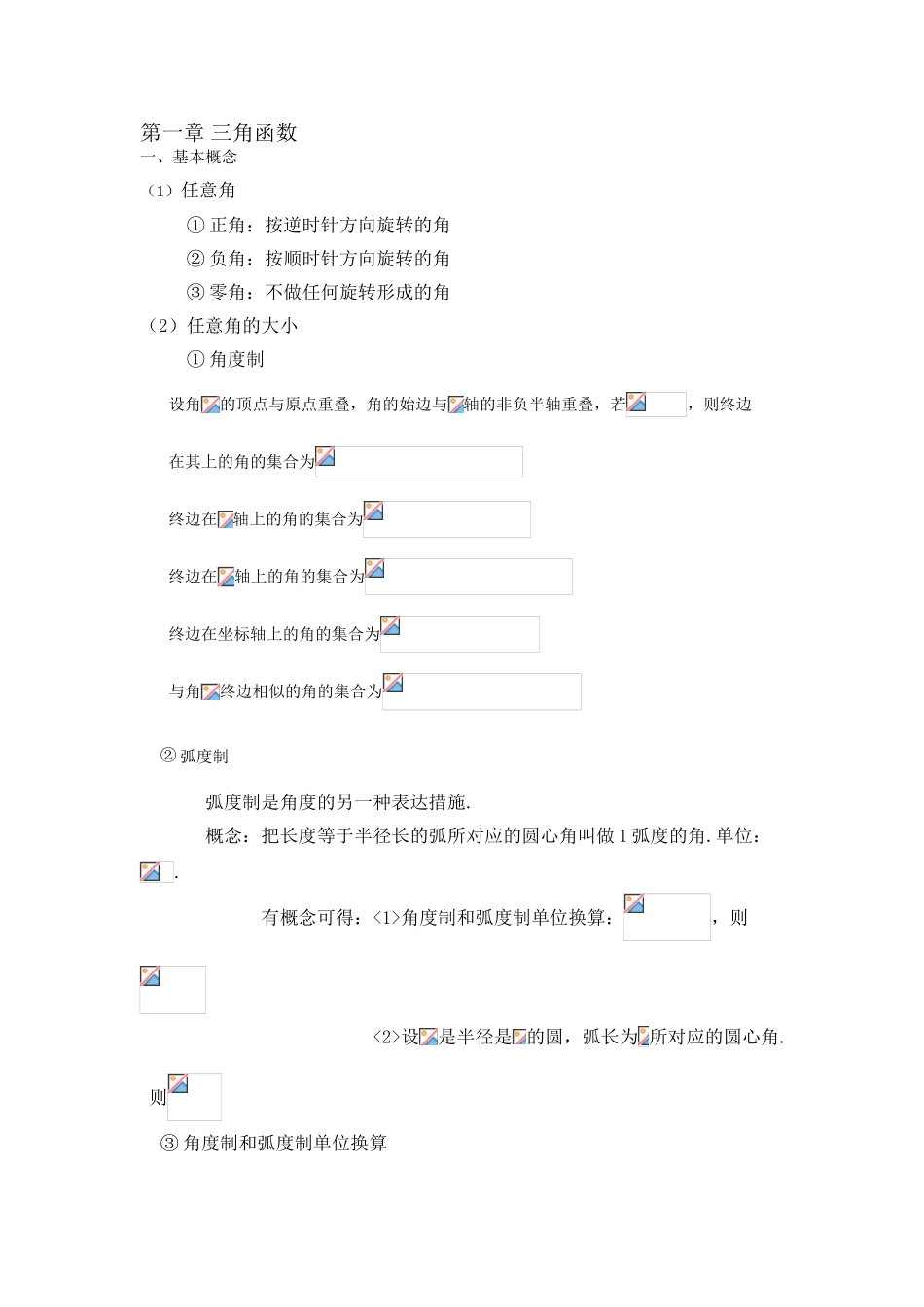
高中数学必修 4 书本知识点 第一章 三角函数一、基本概念(1)任意角 ① 正角:按逆时针方向旋转的角 ② 负角:按顺时针方向旋转的角 ③ 零角:不做任何旋转形成的角(2)任意角的大小 ① 角度制 设角的顶点与原点重叠,角的始边与轴的非负半轴重叠,若,则终边 在其上的角的集合为 终边在轴上的角的集合为 终边在轴上的角的集合为 终边在坐标轴上的角的集合为 与角终边相似的角的集合为 ② 弧度制 弧度制是角度的另一种表达措施. 概念:把长度等于半径长的弧所对应的圆心角叫做 1 弧度的角.单位:. 有概念可得:<1>角度制和弧度制单位换算:,则 <2>设是半径是 的圆,弧长为 所对应的圆心角. 则 ③ 角度制和弧度制单位换算 ,则 常见的角度制和弧度制的转化:(4)象限角(任意角的归类) 设角的顶点与原点重叠,角的始边与轴的非负半轴重叠,终边落在第几象限, 则称为第几象限角. 第一象限角的集合为 第二象限角的集合为 第三象限角的集合为 第四象限角的集合为二、三角函数(1)求三角函数值 设是任意角,它的终边与圆心在原点的圆交于点,那么 、、 ① 特例:若原始单位圆,则、、 ② 终点在轴的角的正切值不存在 ③ 、(★★★★★) ④ 终边相似的角的同一三角函数值相等. 即角度弧度 、、 其中 ⑤ 三角函数在各象限的符号: (2)三角函数图像与性质 1) 正弦函数图像 <1>图像来源 ① 描点法(略)② 平移、拉伸A、的图象上所有点向左(右)平移个单位长度,得到函数的图象;再将函数的图象上所有点的横坐标伸长(缩短)到本来的倍(纵坐标不变),得到函数的图象;再将函数的图象上所有点的纵坐标伸长(缩短)到本来的倍(横坐标不变),得到函数的图象B、的图象上所有点的横坐标伸长(缩短)到本来的倍(纵坐标不变),得到函数的图象;再将函数的图象上所有点第一象限+++第二象限+--第三象限--+第四象限-+-向左(右)平移个单位长度,得到函数的图象;再将函数的图象上所有点的纵坐标伸长(缩短)到本来的倍(横坐标不变),得到函数的图象 <2>图像性质 函数的性质: A、.振幅:;B、周期:;C、.频率:;D、相位:; E、初相: F、函数,、为相邻的获得函数最大值与 函数最小值的自变量的取值,则, <3>诱导公式 A、:函数图像周期性 B、:函数图像在任意相距的两个自变量所对应的 函数值互为相反数 C、:函数图像有关原点对称,或者函数图像在 互为相反数...