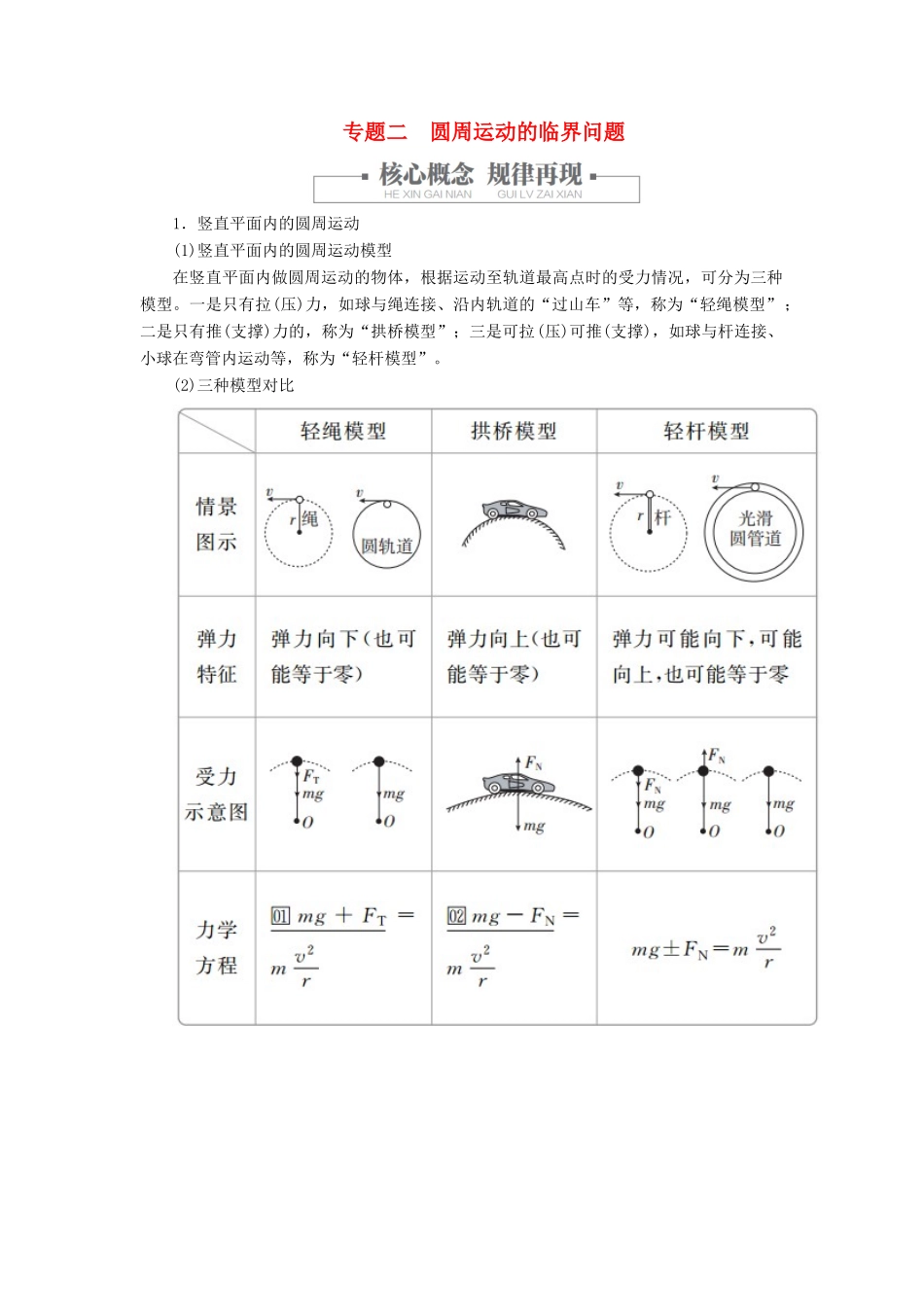
专题二 圆周运动的临界问题1.竖直平面内的圆周运动(1)竖直平面内的圆周运动模型在竖直平面内做圆周运动的物体,根据运动至轨道最高点时的受力情况,可分为三种模型。一是只有拉(压)力,如球与绳连接、沿内轨道的“过山车”等,称为“轻绳模型”;二是只有推(支撑)力的,称为“拱桥模型”;三是可拉(压)可推(支撑),如球与杆连接、小球在弯管内运动等,称为“轻杆模型”。(2)三种模型对比2.水平面内的圆周运动的临界问题水平面内圆周运动的临界问题,其实就是要分析物体所处的状态的受力特点,然后结合圆周运动的知识,列方程求解,一般会涉及临界速度、临界角速度等。通常有下面两种情况:(1)与绳(或面等)的弹力有关的临界问题:此类问题要分析出恰好无弹力或弹力达到最大这一临界状态下的角速度(或线速度)。(2)因静摩擦力而产生的临界问题:此类问题要分析出静摩擦力达到最大时这一临界状态下的角速度(或线速度)。典型考点一 竖直(倾斜)平面内的圆周运动及其临界问题1.(多选)轻绳一端固定在光滑水平轴 O 上,另一端系一质量为 m 的小球,在最低点给小球一初速度,使其在竖直平面内做圆周运动,且刚好能通过最高点 P。下列说法正确的是( )A.小球在最高点时对绳的拉力为零B.小球在最高点时对绳的拉力大小为 mgC.若增大小球的初速度,则过最高点时球对绳的力一定增大D.若增大小球的初速度,则在最低点时球对绳的力一定增大答案 ACD解析 在最高点小球可能受重力和绳的拉力作用,合力提供圆周运动的向心力,由 T+mg=m 知,速度越大绳的拉力越大,速度越小绳的拉力越小,绳的拉力有最小值 0,故速度有最小值,因为小球恰好能通过最高点,故在最高点时的速度为,此时绳的拉力为 0,所以 A 正确,B 错误;根据牛顿第二定律,在最高点时有 T+mg=m,小球初速度增大,则在最高点速度增大,则绳的拉力增大,所以 C 正确;小球在最低点时,合力提供圆周运动的向心力,有 T-mg=m,增大小球的初速度时,小球所受绳的拉力增大,所以 D 正确。2.(多选)当汽车通过圆弧形凸形桥时,下列说法中正确的是( )A.汽车在通过桥顶时,对桥的压力一定小于汽车的重力B.汽车在通过桥顶时,速度越小,对桥的压力就越小C.汽车所需的向心力由桥对汽车的支持力来提供D.汽车通过桥顶时,若汽车的速度 v=(g 为重力加速度,R 为圆弧形桥面的半径),则汽车对桥顶的压力为零答案 AD解析 汽车过凸形桥时,在桥顶有 mg-FN=m,所以 mg>...