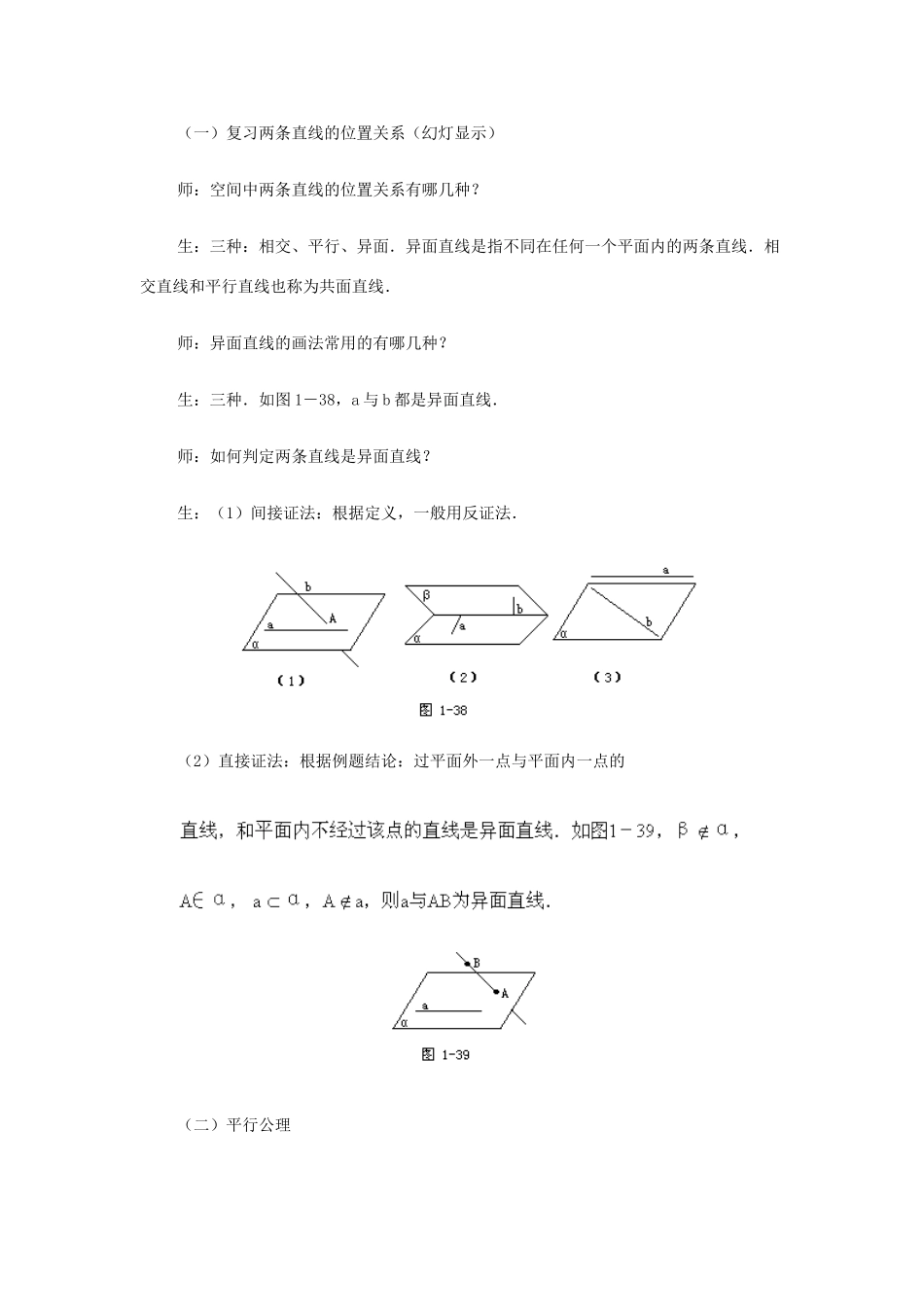
平行直线 一、素质教育目标(一)知识教学点1.公理 4,即平行公理.2.等角定理及推论.(二)能力训练点1.利用联想的方法,掌握并应用由平面内引伸到空间中的平行公理.2.充分利用构造的方法证明等角定理,为下一节两条异面直线所成的角的定义提供了可能性与唯一性.3.通过本节课的学习,让学生认识到在平面几何中成立的结论或定理等,在用于非平面图形时,须先证明.二、教学重点、难点、疑点及解决方法1.教学重点:让学生掌握平行公理及其应用.2.教学难点:等角定理证明的掌握及其应用.3.教学疑点:正确理解等角定理中命题的条件:两个角的两边分别平行且这两个角的方向相同.三、课时安排1 课时.四、教与学的过程设计(一)复习两条直线的位置关系(幻灯显示)师:空间中两条直线的位置关系有哪几种?生:三种:相交、平行、异面.异面直线是指不同在任何一个平面内的两条直线.相交直线和平行直线也称为共面直线.师:异面直线的画法常用的有哪几种?生:三种.如图 1-38,a 与 b 都是异面直线.师:如何判定两条直线是异面直线?生:(1)间接证法:根据定义,一般用反证法.(2)直接证法:根据例题结论:过平面外一点与平面内一点的(二)平行公理师:在平面几何中,如图 1-40,若 a∥b,c∥b,则 a 与 c 平行吗?生:平行.师:也就是说,在平面中,若两条直线 a、c 都和第三条直线 b 平行,则 a∥c.这个命题在空间中是否成立呢?师:实际上,在空间中,若 a∥b,c∥b,则 a∥c 也成立.我们把这个结论作为一个公理,不必证明,可直接应用.平行公理:平行于同一条直线的两条直线互相平行.如图 1-41,三棱镜的三条棱,若 AA′∥BB′,CC′∥BB′,则有 AA′∥CC′.下面请同学们完成下列的例题,巩固应用平行公理.例已知四边形 ABCD 是空间四边形(四个顶点不共面的图 1-41 四边形),E、H 分别是边 AB、AD 的中点,F、G 分别是边 CB、CD师分析:要证明四边形 EFGH 是梯形,即要证明四边形 EFGH 的一组对边平行,另一组对边不平行;或证明一组对边平行且不相等.具体用哪一种方法,我们来分析一下题意:E、H 分别是边 AB、AD 的中证明:如图 1-42,连结 BD. EH 是△ABD 的中位线,根据公理 4,EH∥FG,又 FG>EH,∴四边形 EFGH 是梯形.(三)等角定理师:平行公理不仅是今后论证平行问题的主要依据,也是证明等角定理的基础.等角定理:如果一个角的两边和另一个角...