2014届高三数学总复习 选修4-1圆的进一步认识教案 新人教A版

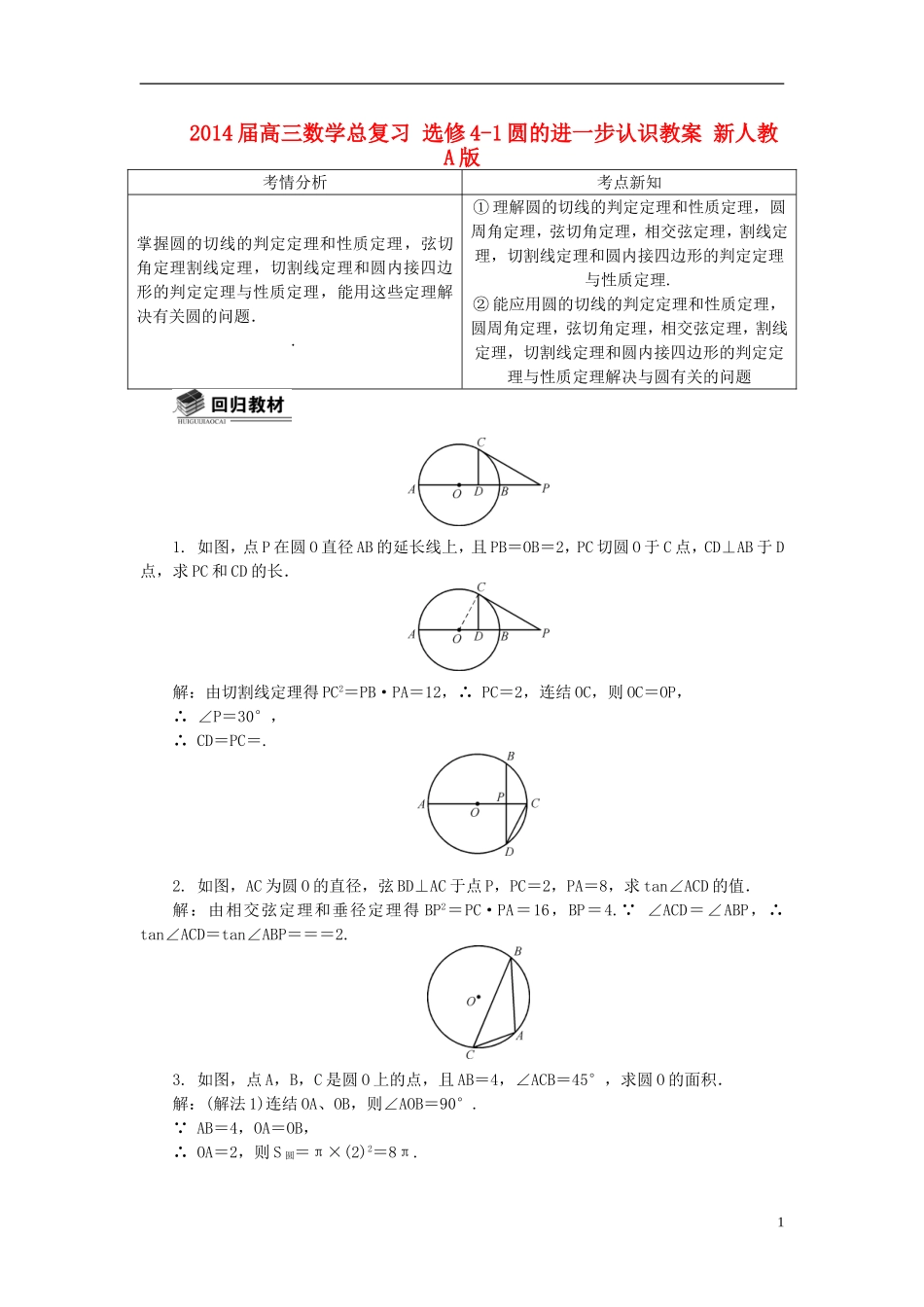
2014 届高三数学总复习 选修 4-1 圆的进一步认识教案 新人教A 版考情分析考点新知掌握圆的切线的判定定理和性质定理，弦切角定理割线定理，切割线定理和圆内接四边形的判定定理与性质定理，能用这些定理解决有关圆的问题．.① 理解圆的切线的判定定理和性质定理，圆周角定理，弦切角定理，相交弦定理，割线定理，切割线定理和圆内接四边形的判定定理与性质定理.② 能应用圆的切线的判定定理和性质定理，圆周角定理，弦切角定理，相交弦定理，割线定理，切割线定理和圆内接四边形的判定定理与性质定理解决与圆有关的问题1. 如图，点 P 在圆 O 直径 AB 的延长线上，且 PB＝OB＝2，PC 切圆 O 于 C 点，CD⊥AB 于 D点，求 PC 和 CD 的长．解：由切割线定理得 PC2＝PB·PA＝12，∴ PC＝2，连结 OC，则 OC＝OP，∴ ∠P＝30°，∴ CD＝PC＝.2. 如图，AC 为圆 O 的直径，弦 BD⊥AC 于点 P，PC＝2，PA＝8，求 tan∠ACD 的值．解：由相交弦定理和垂径定理得 BP2＝PC·PA＝16，BP＝4. ∠ACD＝∠ABP，∴ tan∠ACD＝tan∠ABP＝＝＝2.3. 如图，点 A，B，C 是圆 O 上的点，且 AB＝4，∠ACB＝45°，求圆 O 的面积．解：(解法 1)连结 OA、OB，则∠AOB＝90°. AB＝4，OA＝OB，∴ OA＝2，则 S 圆＝π×(2)2＝8π.1(解法 2)2R＝＝4R＝2，则 S 圆＝π×(2)2＝8π.4. 如图，点 B 在圆 O 上， M 为直径 AC 上一点，BM 的延长线交圆 O 于 N，∠BNA＝45°，若圆 O 的半径为 2 ，OA＝OM，求 MN 的长．解： ∠BNA＝45°，∴ ∠BOA＝90°. OM＝2，BO＝2，∴ BM＝4. BM·MN＝CM·MA＝(2＋2)(2－2)＝8，∴ MN＝2.5. 如图，已知 P 是圆 O 外一点，PD 为圆 O 的切线，D 为切点，割线 PEF 经过圆心 O，若 PF＝12，PD＝4 ，求圆 O 的半径长和∠EFD 的大小．解：由切割线定理，得 PD2＝PE·PFPE＝＝＝4EF＝8，OD＝4. OD⊥PD，OD＝PO，∴ ∠P＝30°，∠POD＝60°，∴∠PDE＝∠EFD＝30°.1. 圆周角定理(1) 圆周角定理：圆周角的度数等于其所对弧度数的一半．(2) 推论 1：同弧(或等弧)上的圆周角相等．同圆或等圆中，相等的圆周角所对的弧相等．(3) 半圆(或直径)上的圆周角等于 90°.反之，90°的圆周角所对的弦为直径．2. 圆的切线(1) 圆的切线的性质与判定① 切线的定义：当直线与圆有 2 个公共点时，直线与圆相交；当直线与圆有且只有 1 ...