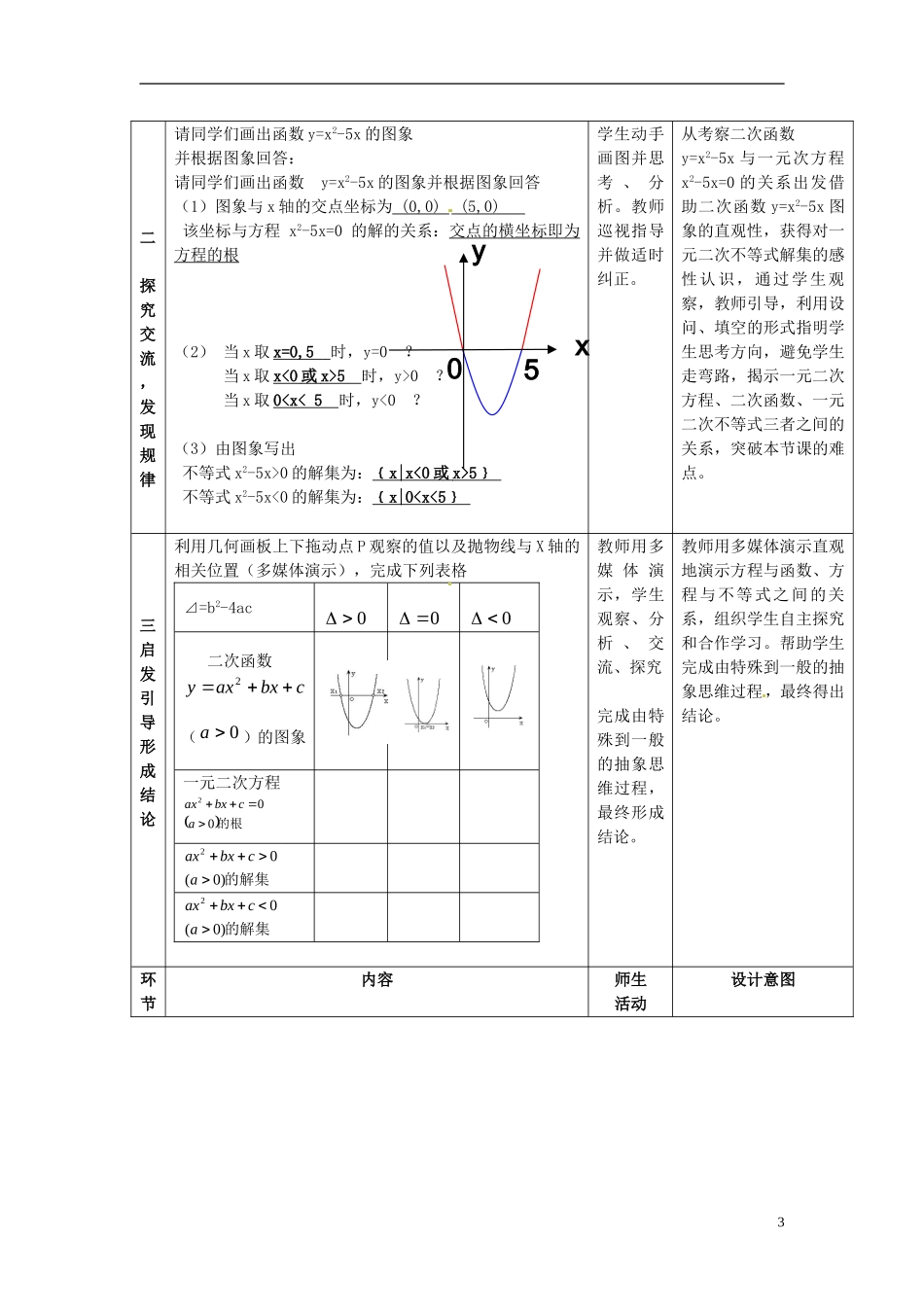
一元二次不等式的解法(第一课时)说课稿一、教材分析1、教学内容本节课是人教版普通高中课程标准实验教科书数学必修5第三章第二节《一元二次不等式及其解法》第1课时。2、教材地位和作用从内容上看它是我们初中学过的一元一次不等式的延伸,同时它也与一元二次方程、二次函数之间联系紧密,涉及的知识面较多。从思想层面看,本节课突出本现了数形结合思想。同时一元二次不等式是解决函数定义域、值域等问题的重要工具,因此本节课在整个中学数学中具有较重要的地位和作用。3、教学目标知识目标:正确理解一元二次不等式、一元二次方程、二次函数的关系。熟练掌握一元二次不等式的解法。能力目标:培养数形结合思想、抽象思维能力和形象思维能力。思想目标:在教学中渗透由具体到抽象,由特殊到一般,类比猜想、等价转化的数学思想方法。情感目标:通过具体情境,使学生体验数学与实践的紧密联系,感受数学魅力,激发学生求知欲望。4、重难点重点:一元二次不等式的解法。难点:一元二次方程,一元二次不等式与二次函数的关系。二、教法探讨 1、选择教法的原则和依据 根据学生的原有知识和现有的认知规律,以发展学生的能力和应试水平为原则。 2、教法选择 探究、启发诱导法,分层教学法。重点以引导学生为主,让学生积极主动的参与到新知识的探究中去。三、学法分析结合本节内容和学生实际,适当引入研究性学习,采用讲练结合方法,通过阅读发现问题,分析探索,合作交流最终形成技能。使学生在观察、思考、交流中体验数学学习的乐趣。四、教学设计环节内容师生活动设计意图引例 1、(幻灯片)(1)如何作一元一次函数 y=2x-7 图象? 令 x=0 则 y=-7,得到点(0,-7) 令 y=0 则 x=-3.5,得到点(3.5,0)经过两点作直线即得函数 y=2x-7 的图象,如图: 学生动手操 作 画图。教师适当帮助同学回顾一次函数图象的画法。引导学生设计问题刺激学生回忆自己已有的知识和技能。以学生熟悉的画一次函数图象入手,使学生自觉地把一次函数图象与一次方程以及一次函数紧密联系起来,从而感受函数与方程、函数与173.5yxo一创设情境,引入新课(2)根据图象回答:X 取 x=3.5 时, y=0 即 2x-7=0X 取 x>3.5 时, y>0 即 2x-7>0X 取 x<3.5 时, y<0 即 2x-7<0 (3)根据图象回答不等式 2x-7>0 的解集为:{x| x>3.5}不等式 2x-7<0 的解集为:{x| x<3.5}不等式 2x-7≥0 的解集为:{x| x≥3.5}不等式 2x-7...