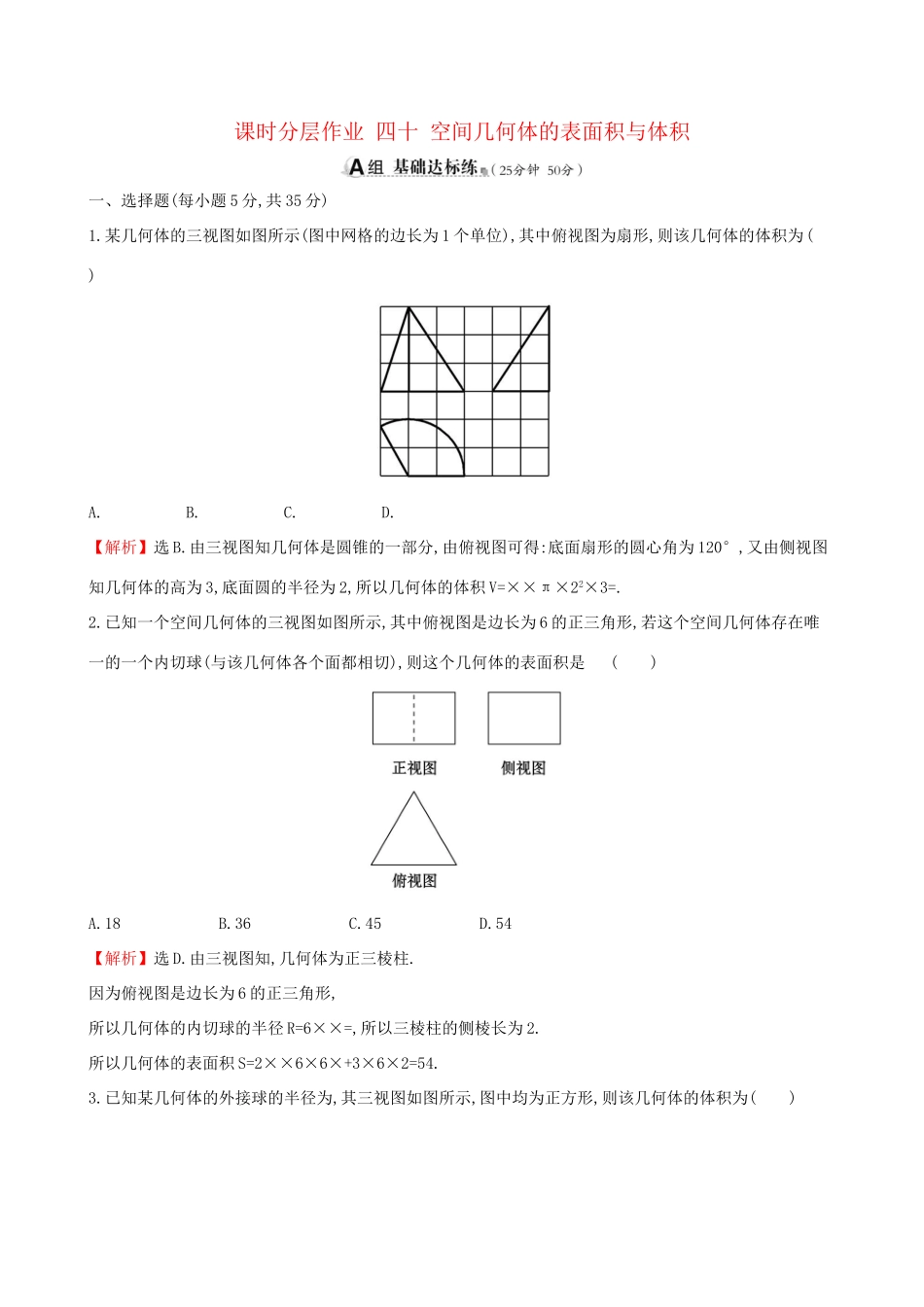
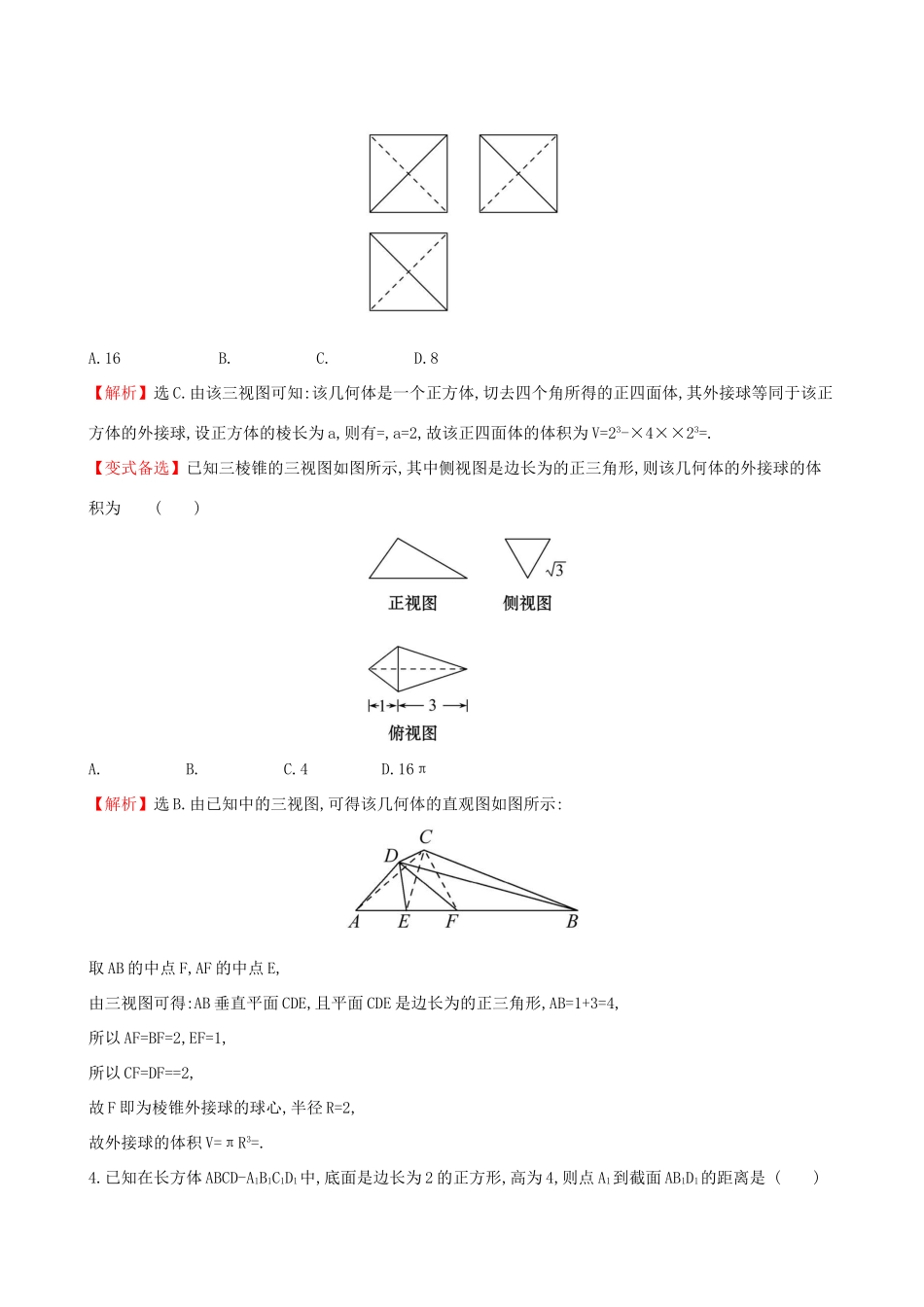
课时分层作业四十空间几何体的表面积与体积一、选择题(每小题5分,共35分)1.某几何体的三视图如图所示(图中网格的边长为1个单位),其中俯视图为扇形,则该几何体的体积为()A.B.C.D.【解析】选B.由三视图知几何体是圆锥的一部分,由俯视图可得:底面扇形的圆心角为120°,又由侧视图知几何体的高为3,底面圆的半径为2,所以几何体的体积V=××π×22×3=.2.已知一个空间几何体的三视图如图所示,其中俯视图是边长为6的正三角形,若这个空间几何体存在唯一的一个内切球(与该几何体各个面都相切),则这个几何体的表面积是()A.18B.36C.45D.54【解析】选D.由三视图知,几何体为正三棱柱.因为俯视图是边长为6的正三角形,所以几何体的内切球的半径R=6××=,所以三棱柱的侧棱长为2.所以几何体的表面积S=2××6×6×+3×6×2=54.3.已知某几何体的外接球的半径为,其三视图如图所示,图中均为正方形,则该几何体的体积为()A.16B.C.D.8【解析】选C.由该三视图可知:该几何体是一个正方体,切去四个角所得的正四面体,其外接球等同于该正方体的外接球,设正方体的棱长为a,则有=,a=2,故该正四面体的体积为V=23-×4××23=.【变式备选】已知三棱锥的三视图如图所示,其中侧视图是边长为的正三角形,则该几何体的外接球的体积为()A.B.C.4D.16π【解析】选B.由已知中的三视图,可得该几何体的直观图如图所示:取AB的中点F,AF的中点E,由三视图可得:AB垂直平面CDE,且平面CDE是边长为的正三角形,AB=1+3=4,所以AF=BF=2,EF=1,所以CF=DF==2,故F即为棱锥外接球的球心,半径R=2,故外接球的体积V=πR3=.4.已知在长方体ABCD-A1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是()A.B.C.D.【解析】选C.设点A1到截面AB1D1的距离是h,由=,可得·h=·AA1,解得h=.【一题多解】选C.取B1D1的中点E1,连接A1E1,AE1,根据几何体的结构特征,可知,作A1H⊥AE1,垂足为H,A1H⊥平面AB1D1,A1H即为所求.A1E1=,A1A=4,A1A⊥A1E1,A1H=(等面积法).【变式备选】如图,在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,M,N分别为AB,PC的中点,PD=AD=2,AB=4.则点A到平面PMN的距离为____________.【解析】取PD的中点E,连接AE,NE,则因为四棱锥P-ABCD中,底面ABCD是矩形,M,N分别为AB,PC的中点,所以NE∥AM,NE=AM,所以四边形AENM是平行四边形,所以AE∥MN,所以点A到平面PMN的距离等于点E到平面PMN的距离,设为h,在△PMN中,PN=,PM=2,MN=,所以S△PMN=×2×=,由VE-PMN=VM-PEN,可得×h=××1×2×2,所以h=.答案:【方法技巧】求点到平面的距离(1)能作出高线的则直接作出高线,转化为求线段的长度;(2)不能直接求时,①可转化为与平面平行的直线上一点到平面的距离.②或利用等体积法求解.5.已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为()A.36πB.64πC.144πD.256π【解析】选C.如图所示,当点C位于垂直于面AOB的直径端点时,三棱锥O-ABC的体积最大,设球O的半径为R,此时VO-ABC=VC-AOB=×R2×R=R3=36,故R=6,则球O的表面积为S=4πR2=144π.6.某几何体的三视图如图所示,其内切球的体积为()A.πB.πC.πD.π【解析】选A.根据图示可得几何体为正八面体,内切球心为O,过O作OH垂直AD于点H,连接S1H,作OR垂直S1H,OR即为内切球O的半径.所以R=,V0=π.7.如图,在透明塑料制成的长方体ABCD-A1B1C1D1容器内灌进一些水(未满),现将容器底面一边BC固定在底面上,再将容器倾斜,随着倾斜度的不同,有下列四种说法:①水的部分始终呈棱柱状;②水面四边形EFGH的面积为定值;③棱A1D1始终与水面EFGH平行;④若E∈AA1,F∈BB1,则AE+BF是定值.则其中正确命题的个数是()A.1个B.2个C.3个D.4个【解析】选C.结合题设中提供的图形信息可知:当容器底面一边BC固定时,BC∥FG∥A1D1,故由线面平行的判定定理可知结论“棱A1D1始终与水面EFGH平行”成立;同时由于四边形ABFE≌四边形DCGH,且互相平行,则由棱柱的定义可知结论“水的部分始终呈棱柱状”正确;如图,由于水平放置时,水的高度是定值,所以当一部分上升的同时,另一面下降相同的高度,因为BF=h-FD,AE=h+D1E且FD=D1E,所以BF+AE=h-FD+h+D1E=2h(定值),即结论“若E∈AA1,F∈BB1,则AE+BF是定值”是正确的;因为...