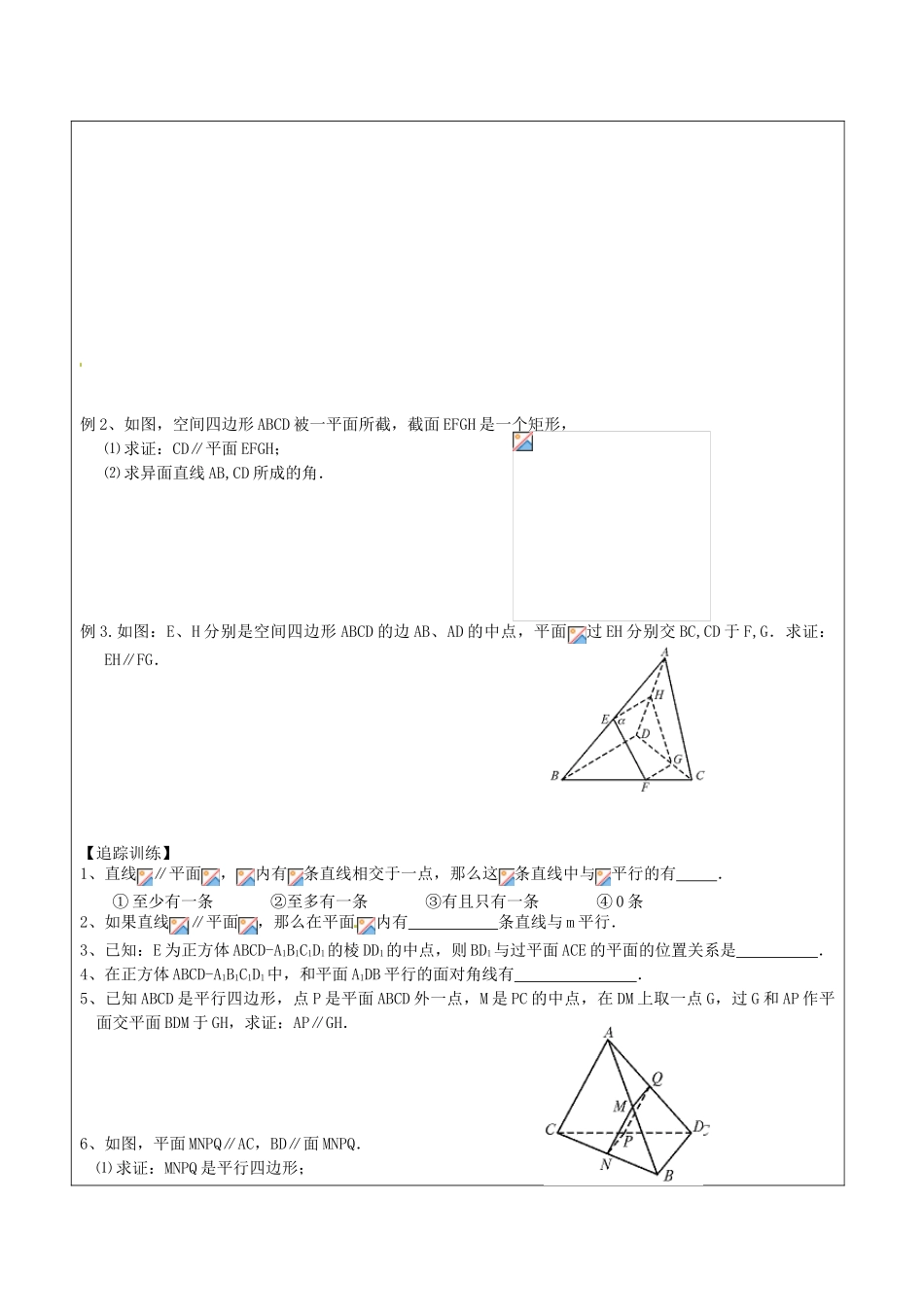
江苏省邳州市第四中学高中数学 线面平行的习题课导学案 苏教版必修 2 主备教师: 任课教师: 时间:2013 年 9 月 日【小题训练】1、下列说法正确的是 .① 平面和平面只有一个公共点 ②两两相交的三条直线共面③ 不共面的四点中,任何三点不共线 ④有三个公共点的两平面必重合2、在空间内,可以确定一个平面的条件是 .① 三个点 ②两条直线 ③一个点和一条直线 ④不共点的两两相交的三条直线3、异面直线是指 .① 空间中两条不相交的直线 ②平面内的一条直线与平面外的一条直线③ 分别位于两个不同平面内的两条直线 ④不同在任何一个平面内的两条直线4、在立体几何中,下列命题中正确的是 .① 垂直于同一直线的两直线平行 ②到定点距离等于定长的点的轨迹是圆③ 有三个角是直角的四边形是矩形 ④自一点向一已知直线引垂线有且只有一条5、a,b 是两条异面直线,下列结论正确的是 .① 过不在 a,b 上的任一点,可作一个平面与a,b 平行② 过不在 a,b 上的任一点,可作一条直线与 a,b 相交③ 过不在 a,b 上的任一点,可作一条直线与 a,b 都平行④ 过 a 可以 并且只可以作一平面与 b 平行6、半圆绕着它的直径所在的直线旋转一周所得的几何体是 .7、“点 A 在直线上 ,在平面外”用符号表示为 .8、果 OA∥O1A1,OB∥O1B1,那么∠AOB 与∠A1O1B1 .9、如果两条直线和没有公共点,那么两直线的位置关系是 .10、已知:正方体 ABCD-A1B1C1D 1中,E 是 DD1的中点.求证:BD1∥平面 ACE.【经典范例】例 1、已知 AB,CD 为异面线段,E,F 分别为 AC,BD 中点,过 E,F作平面∥AB.⑴ 求证:CD∥; ⑵ 若 AB=4,EF=,CD=2,求 AB 与 CD 所成角.例 2、如图,空间四边形 ABCD 被一平面所截,截面 EFGH 是一个矩形,⑴ 求证:CD∥平面 EFGH;⑵ 求异面直线 AB,CD 所成的角.例 3.如图:E、H 分别是空间四边形 ABCD 的边 AB、AD 的中点,平面过 EH 分别交 BC,CD 于 F,G.求证:EH∥FG.【追踪训练】1、直线∥平面,内有条直线相交于一点,那么这条直线中与平行的有 .① 至少有一条 ②至多有一条 ③有且只有一条 ④ 0 条2、如果直线∥平面,那么在平面内有 条直线与 m 平行.3、已知:E 为正方体 ABCD-A1B1C1D1的棱 DD1的中点,则 BD1与过平面 ACE 的平面的位置关系是 .4、在正方体 ABCD-A1B1C1D1中,和平面 A1DB 平行的面对...