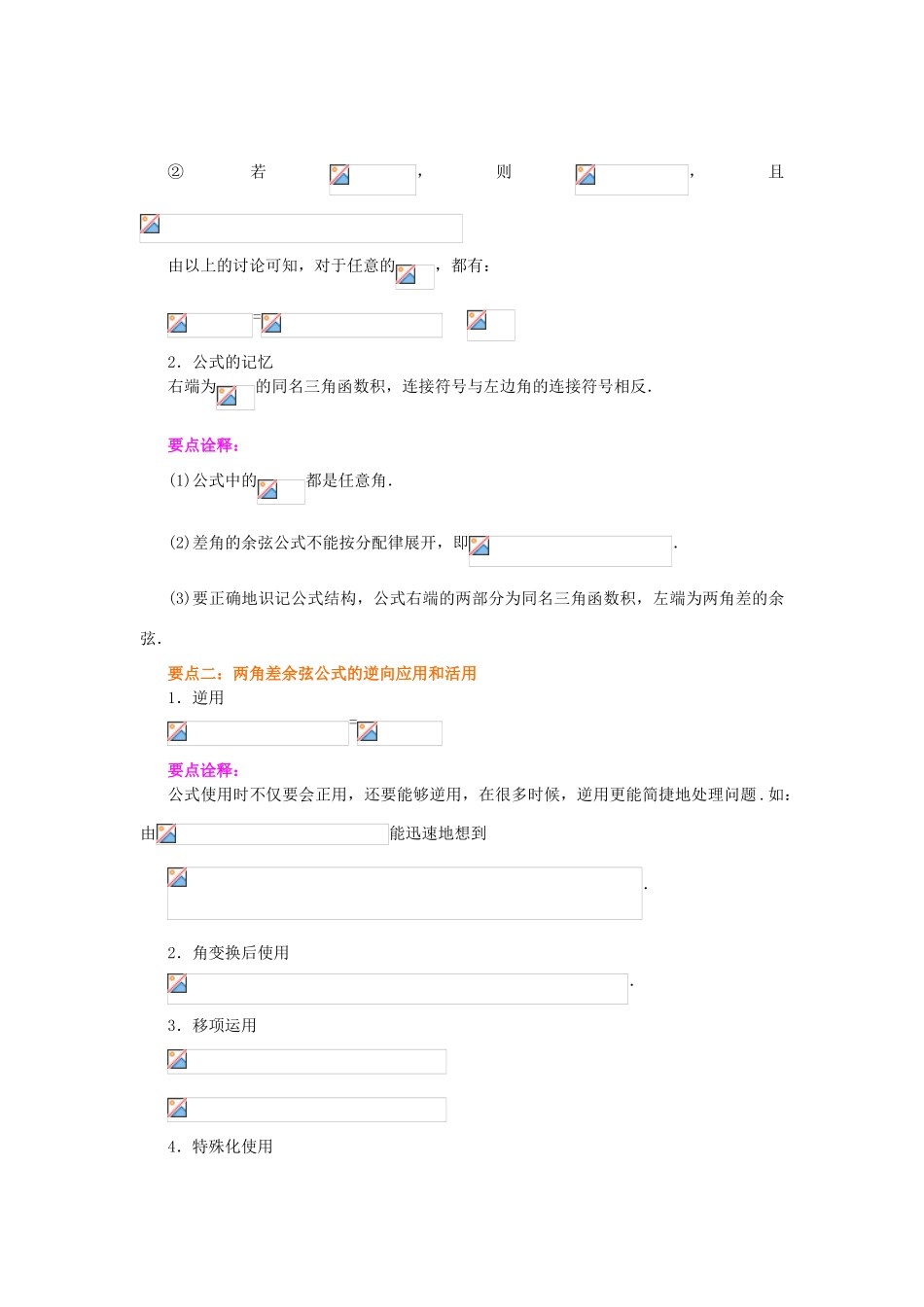
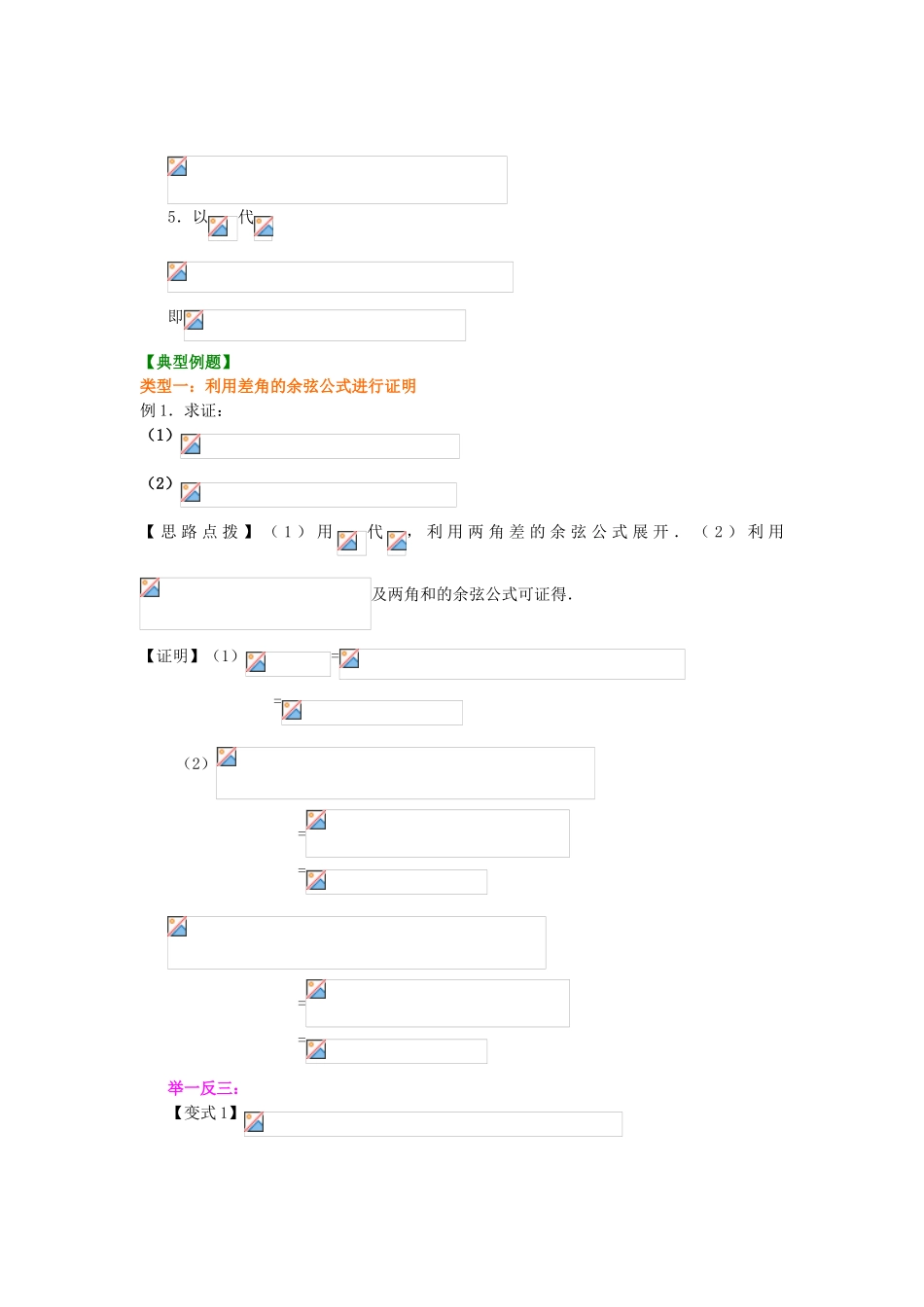
两角差的余弦公式(提高)【学习目标】1.经历用向量的数量积推导出两角差的余弦公式的过程,进一步体会向量方法的作用.2.通过公式的推导,领会其中的数学基本思想,掌握研究数学的基本方法,从而提高数学素质.【要点梳理】要点一:两角差的余弦公式1.两角差的余弦公式的推导:(1)如图,在平面直角坐标系内作单位圆,以为始边作角,它们的终边与单位圆的交点分别为,则由向量数量积的概念,有,结合向量数量积的坐标表示,有所以= (*)(2)由以上的推导过程可知,是任意角,则也应为任意角,但由两个向量数量积的意义,(*)中的.为此,我们讨论如下:由 于是 任 意 角 , 由 诱 导 公 式 , 总 可 以 找 到 一 个 角, 使.① 若,则.②若,则,且由以上的讨论可知,对于任意的,都有:= 2.公式的记忆右端为的同名三角函数积,连接符号与左边角的连接符号相反.要点诠释:(1)公式中的都是任意角.(2)差角的余弦公式不能按分配律展开,即.(3)要正确地识记公式结构,公式右端的两部分为同名三角函数积,左端为两角差的余弦.要点二:两角差余弦公式的逆向应用和活用1.逆用 =要点诠释:公式使用时不仅要会正用,还要能够逆用,在很多时候,逆用更能简捷地处理问题 .如:由能迅速地想到.2.角变换后使用.3.移项运用4.特殊化使用5.以代即【典型例题】类型一:利用差角的余弦公式进行证明例 1.求证:(1)(2)【 思 路 点 拨 】 ( 1 ) 用代, 利 用 两 角 差 的 余 弦 公 式 展 开 . ( 2 ) 利 用及两角和的余弦公式可证得.【证明】(1)= = (2) = = = =举一反三:【变式 1】证明: = = = = =类型二:利用差角的余弦公式化简三角函数式例 2.(1);(2).【解析】(1)原式.(2)原式= = = = =【总结升华】 两角差的余弦公式中,,可以是单个角,也可以是两个角的和或差,在运用公式时常将两角的和或差视为一个整体,如(2)题的()可视为一个整体.分析题目特点,构造两角的差,然后应用两角差的余弦公式,是常见题型.举一反三:【变式 1】(1)cos15°cos105°+sin15°sin105°;(2)cos(-35)°·cos(25°+)+sin(-35°)·sin(25°+);(3)cos 40°cos70°+cos20°cos50°;(4);【解析】(1)原式=cos(15°-105°)=cos(-90°)=0.(2)原式.(3)原式.(4)原式 类型三:利用差角的余弦公式求值(或角)例 3.已知,,,均为锐角...