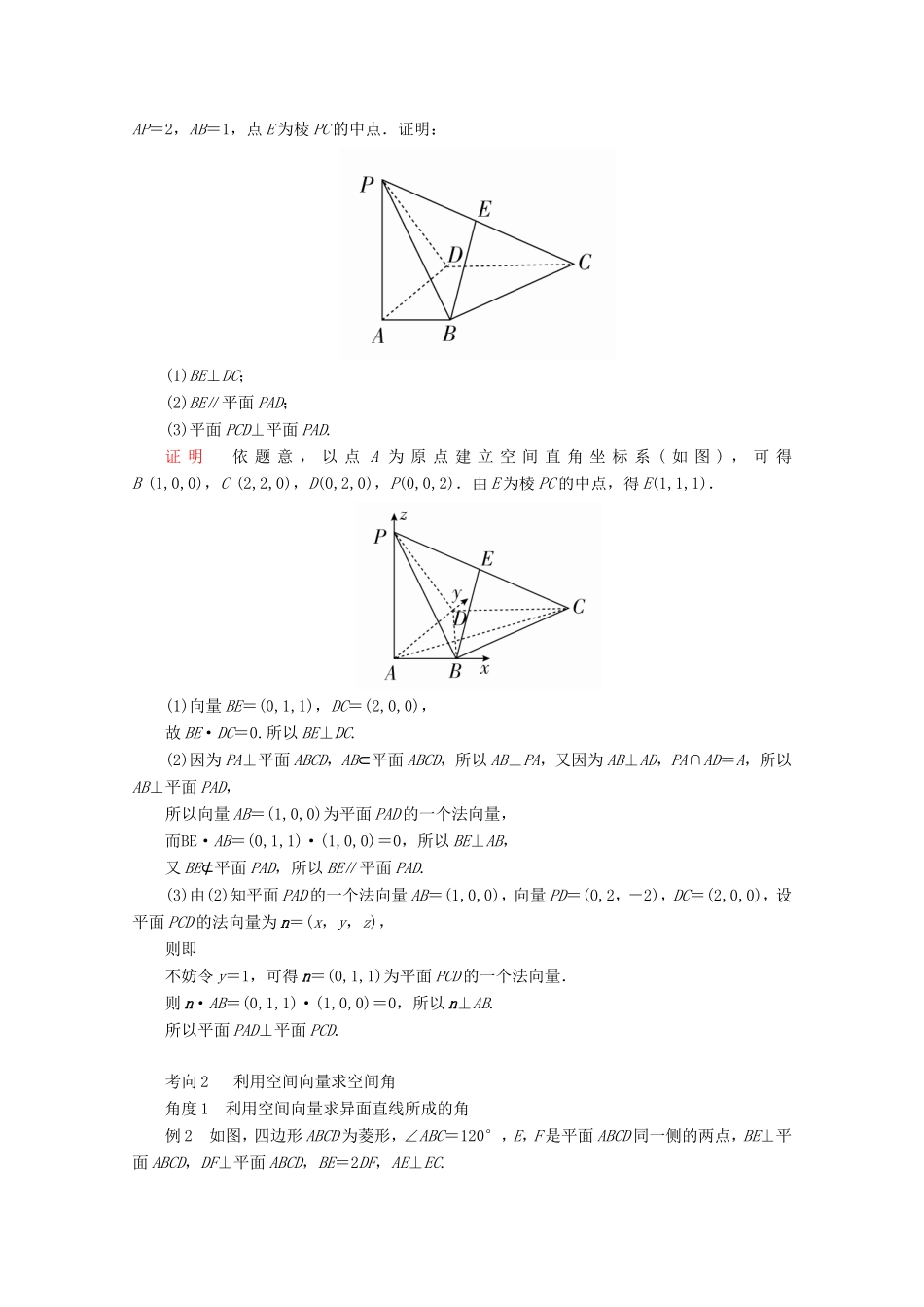
第3讲立体几何中的向量方法「考情研析」以空间几何体为载体考查空间角是高考命题的重点,常与空间线面关系的证明相结合,热点为二面角的求解,均以解答题的形式进行考查,难度主要体现在建立空间直角坐标系和准确计算上.核心知识回顾1.线、面的位置关系与向量的关系设直线l,m的方向向量分别为a=(a1,b1,c1),b=(a2,b2,c2).平面α,β的法向量分别为μ=(a3,b3,c3),v=(a4,b4,c4).(1)l∥m⇒a∥b⇔a=kb⇔□a1=ka2,b1=kb2,c1=kc2;(2)l⊥m⇔a⊥b⇔a·b=□0⇔□a1a2+b1b2+c1c2=0;(3)l∥α⇔a⊥μ⇔a·μ=□0⇔□a1a3+b1b3+c1c3=0;(4)l⊥α⇔a∥μ⇔a=kμ⇔□a1=ka3,b1=kb3,c1=kc3;(5)α∥β⇔μ∥v⇔μ=kv⇔□a3=ka4,b3=kb4,c3=kc4;(6)α⊥β⇔μ⊥v⇔μ·v=□0⇔□a3a4+b3b4+c3c4=0.2.三种空间角与空间向量的关系(1)线线角:设a,b分别为异面直线a,b的方向向量,则两异面直线所成的角θ满足cosθ=□.(2)线面角:设l是斜线l的方向向量,n是平面α的法向量,则斜线l与平面α所成的角θ满足sinθ=□.(3)二面角①如图(Ⅰ),AB,CD是二面角α-l-β的两个半平面内与棱l垂直的直线,则二面角的大小θ=□〈AB,CD〉;②如图(Ⅱ)(Ⅲ),n1,n2分别是二面角α-l-β的两个半平面α,β的法向量,则二面角的大小θ满足cosθ=□-cos〈n1,n2〉或cos〈n1,n2〉.热点考向探究考向1利用向量证明平行与垂直例1如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E,E1分别是棱AD,AA1的中点.(1)设F是棱AB的中点,证明:直线EE1∥平面FCC1;(2)证明:平面D1AC⊥平面BB1C1C.证明如图,过点D作AB垂线交AB于G,则以D为原点,DG,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,易得A(,-1,0),B(,3,0),C(0,2,0),E1(,-1,1),E,F(,1,0),D1(0,0,2),B1(,3,2),C1(0,2,2).(1)CC1=(0,0,2),CF=(,-1,0).设平面C1FC的法向量n1=(x,y,z),则令x=1,得n1=(1,,0),又E1E=,故E1E·n1=0,又E1E⊄平面FCC1,所以E1E∥平面FCC1.(2)D1A=(,-1,-2),D1C=(0,2,-2),设平面D1AC的法向量n2=(a,b,c),由得令b=1,得其中一个n2=(,1,1).同理易得平面BB1C1C的一个法向量n3=(1,-,0),n2·n3=0,故平面D1AC⊥平面BB1C1C.利用空间向量证明平行与垂直的方法步骤(1)建立空间直角坐标系,建系时,要尽可能地利用载体中的垂直关系.(2)建立空间图形与空间向量之间的关系,用空间向量表示出问题中所涉及的点、直线、平面的要素.(3)通过空间向量的运算研究平行、垂直关系.(4)根据运算结果解释相关问题.(2019·贵阳二模)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=2,AB=1,点E为棱PC的中点.证明:(1)BE⊥DC;(2)BE∥平面PAD;(3)平面PCD⊥平面PAD.证明依题意,以点A为原点建立空间直角坐标系(如图),可得B(1,0,0),C(2,2,0),D(0,2,0),P(0,0,2).由E为棱PC的中点,得E(1,1,1).(1)向量BE=(0,1,1),DC=(2,0,0),故BE·DC=0.所以BE⊥DC.(2)因为PA⊥平面ABCD,AB⊂平面ABCD,所以AB⊥PA,又因为AB⊥AD,PA∩AD=A,所以AB⊥平面PAD,所以向量AB=(1,0,0)为平面PAD的一个法向量,而BE·AB=(0,1,1)·(1,0,0)=0,所以BE⊥AB,又BE⊄平面PAD,所以BE∥平面PAD.(3)由(2)知平面PAD的一个法向量AB=(1,0,0),向量PD=(0,2,-2),DC=(2,0,0),设平面PCD的法向量为n=(x,y,z),则即不妨令y=1,可得n=(0,1,1)为平面PCD的一个法向量.则n·AB=(0,1,1)·(1,0,0)=0,所以n⊥AB.所以平面PAD⊥平面PCD.考向2利用空间向量求空间角角度1利用空间向量求异面直线所成的角例2如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.(1)证明:平面AEC⊥平面AFC;(2)求直线AE与直线CF所成角的余弦值.解(1)证明:连接BD,设BD∩AC=G,连接EG,FG,EF.在菱形ABCD中,不妨设GB=1.由∠ABC=120°,可得AG=GC=.由BE⊥平面ABCD,AB=BC,可知AE=EC.又AE⊥EC,所以EG=,且EG⊥AC.在Rt△EBG中,...