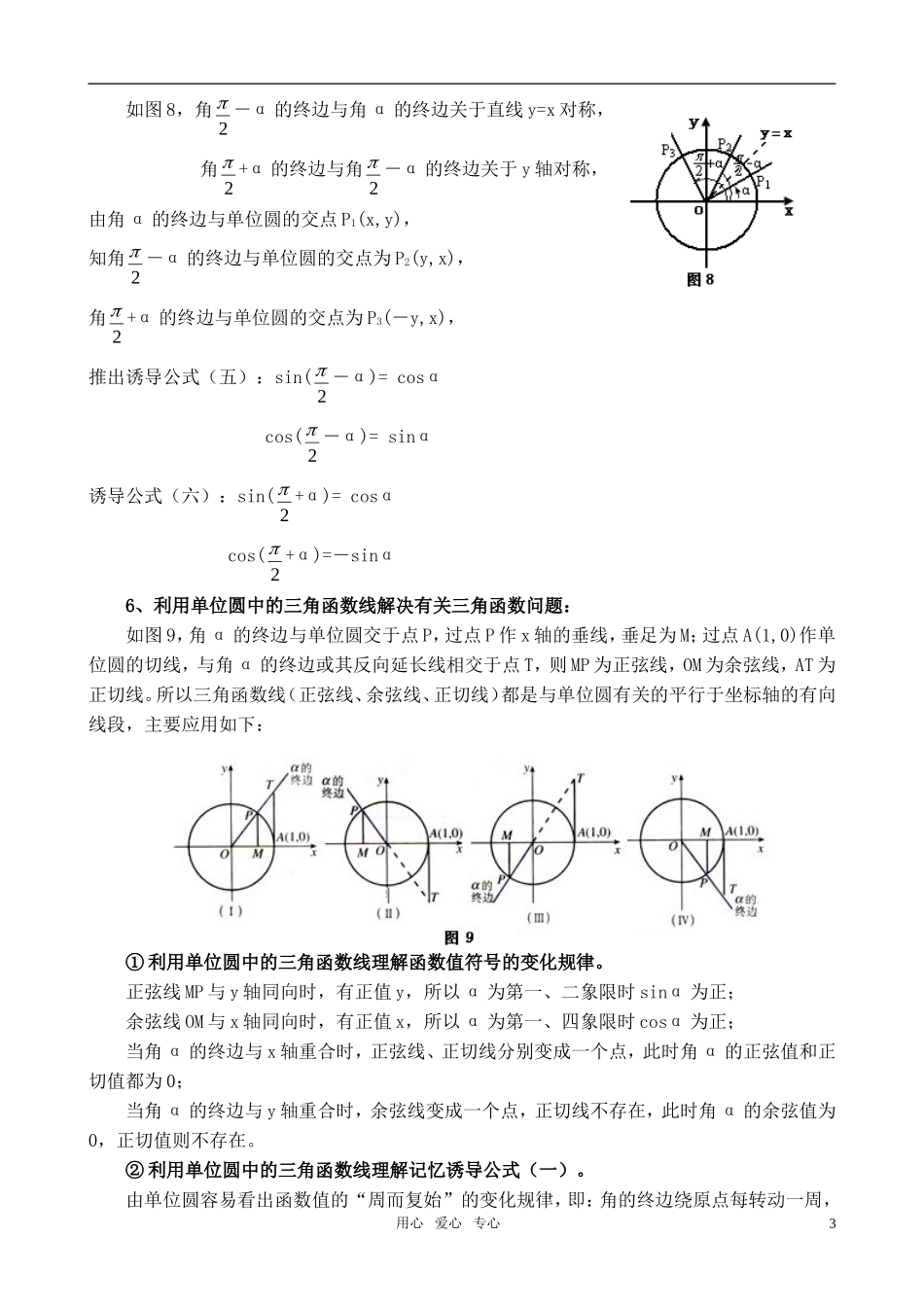
单位圆在高一数学中的应用摘要:象限的符单位圆在学习高一数学、尤其在三角函数中应用广泛,利用单位圆可以:定义任意角的三角函数;理解记忆三角函数值在各个号;巧记特殊角的三角函数值;帮助理解同角三角函数的基本关系;推导三角函数的诱导公式;而且利用单位圆可以解决有关三角函数问题,包括:求三角函数值;解三角函数不等式;求函数定义域;比较三角函数值的大小等等。关键词:单位圆、三角函数、应用 所谓单位圆,就是在直角坐标系中,以原点 O 为圆心,以单位长度为半径的圆。单位圆在高一数学中的应用主要体现在必修④三角函数中的应用,而三角函数在整个高中数学学习乃至高考中所占比重都很大,所以有必要充分利用单位圆来更好地学习掌握这部分知识。 一、单位圆在教材教学中的应用1、利用单位圆定义任意角的三角函数:如图 1,设 α 是一个任意角,它的终边与单位圆交于点 P(x,y),则α 的正弦为: sinα=y,α 的余弦为: cosα=x,α 的正切为: tanα=xy (x≠0)用单位圆上点的坐标来定义三角函数,可以使正弦函数、余弦函数从自变量(角的弧度数)到函数值(单位圆上点的横、纵坐标)之间的对应关系更清楚、简单,突出了三角函数的本质,也使三角函数反映的数形关系更直接,为后面讨论其他问题奠定基础。 2、利用单位圆理解记忆三角函数值在各象限的符号:根据单位圆中三角函数的定义可知,正弦的符号决定于纵坐标 y 的符号,余弦的符号决定于横坐标 x 的符号,正切是由纵坐标 y、横坐标 x 的符号决定:同号为正,异号为负。因此,各三角函数值在每个象限的符号如下图 2: 3、利用单位圆巧记特殊角的三角函数值:用心 爱心 专心1由三角函数定义:sinα=y,cosα=x,tanα=xy (x≠0),结合单位圆(如图 3),便容易理解记忆以下特殊角的三角函数值: α0°90°180°270°360°sinα010-10cosα10-101tanα0不存在0不存在0 4、利用单位圆易于理解同角三角函数的基本关系:在单位圆中构造出以任意角的正弦线、余弦线为直角边的直角三角形,如图 4,由 Rt△OMP 中,MP2+OM2=1,得出同角三角函数的基本关系之一:sinα2+cosα2=1;由 Rt△OMP∽Rt△OAT,OAATOMMP ,得出同角三角函数的基本关系之二:tancossin(α≠k +2 ,k∈Z)。 5、利用单位圆推导三角函数的诱导公式:单位圆具有很好的对称性,通过对单位圆上对称点的坐标的关系来探究推出诱导公式。如图 5,角 +α 的...