二倍角的正弦、余弦、正切VIP免费

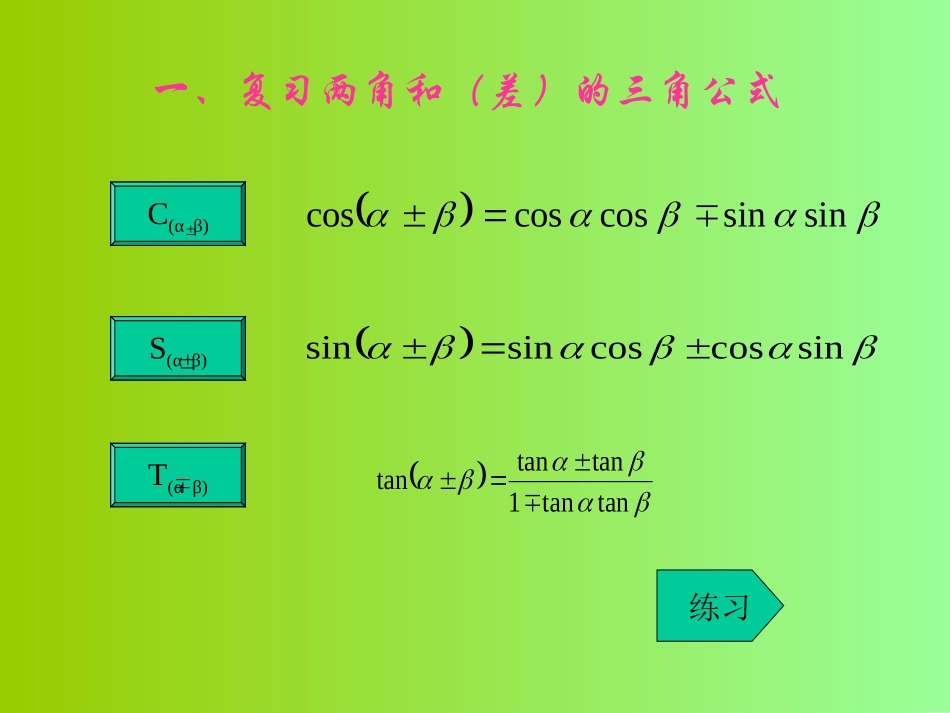
复习复习新课新课例题例题练习练习小结小结作业作业返回返回一、复习两角和（差）的三角公式S(αβ)C(αβ)T(αβ)sinsincoscoscossincoscossinsintantan1tantantan练习0002000000022000015tan115tan165.22tan15.22tan255.7sin5.37cos5.7cos5.37sin475cos75sin2312sin12cos269sin24sin69cos24cos1、、、、、、返回sinsincoscoscos二倍角公式的推导22sincos2cos22sin212cos1cos22cos1cossin22利用变形为cossin22sinsincoscossinsintantan1tantantan2tan1tan22tank2注Zkk4返回例一、（公式巩固性练习）求值：1．sin2230’cos2230’=18cos222.3.8cos8sin224.12cos24cos48cos48sin84245sin210224cos224cos216sin12cos12sin212cos24cos24sin4例二.2365cos125cos125sin222.2sin2cos44cos)2sin2)(cos2sin2(cos2222)125cos125)(sin125cos125(sin1.继续3．4．tan11tan112tantan1tan222coscos21221cos2cos2122例三、若tan=3，求sin2cos2的值57tan11tantan2cossincossincossin2222222解：sin2cos2=例四、条件甲：条件乙：那么甲是乙的什么条件？asin1a2cos2sin解：sin1a2)2cos2(sina|2cos2sin|即当在第三象限时，甲乙；当a>0时，乙甲∴甲既不是乙的充分条件,也不是乙的必要条件。继续例五、（P43例一）已知),2(,135sin求sin2，cos2，tan2的值。cos2=tan2=解：∵),2(,135sin∴1312sin1cos2∴sin2=2sincos=169120169119sin212119120返回的值是？、4cos2sin212的值为？则、若tan1tan,2cossin2_______52cos5cos3、27254、若_______sin1sin1，则练习2cos32412sin2返回1、二倍角公式是和角公式的特例，体现将一般化归为特殊的基本数学思想方法。2、二倍角公式与和角、差角公式一样，反映的都是如何用单角的三角函数值表示复角（和、差、倍）的三角函数值，结合前面学习到的同角三角函数关系式和诱导公式可以解决三角函数中有关的求值、化简和证明问题。归纳总结返回