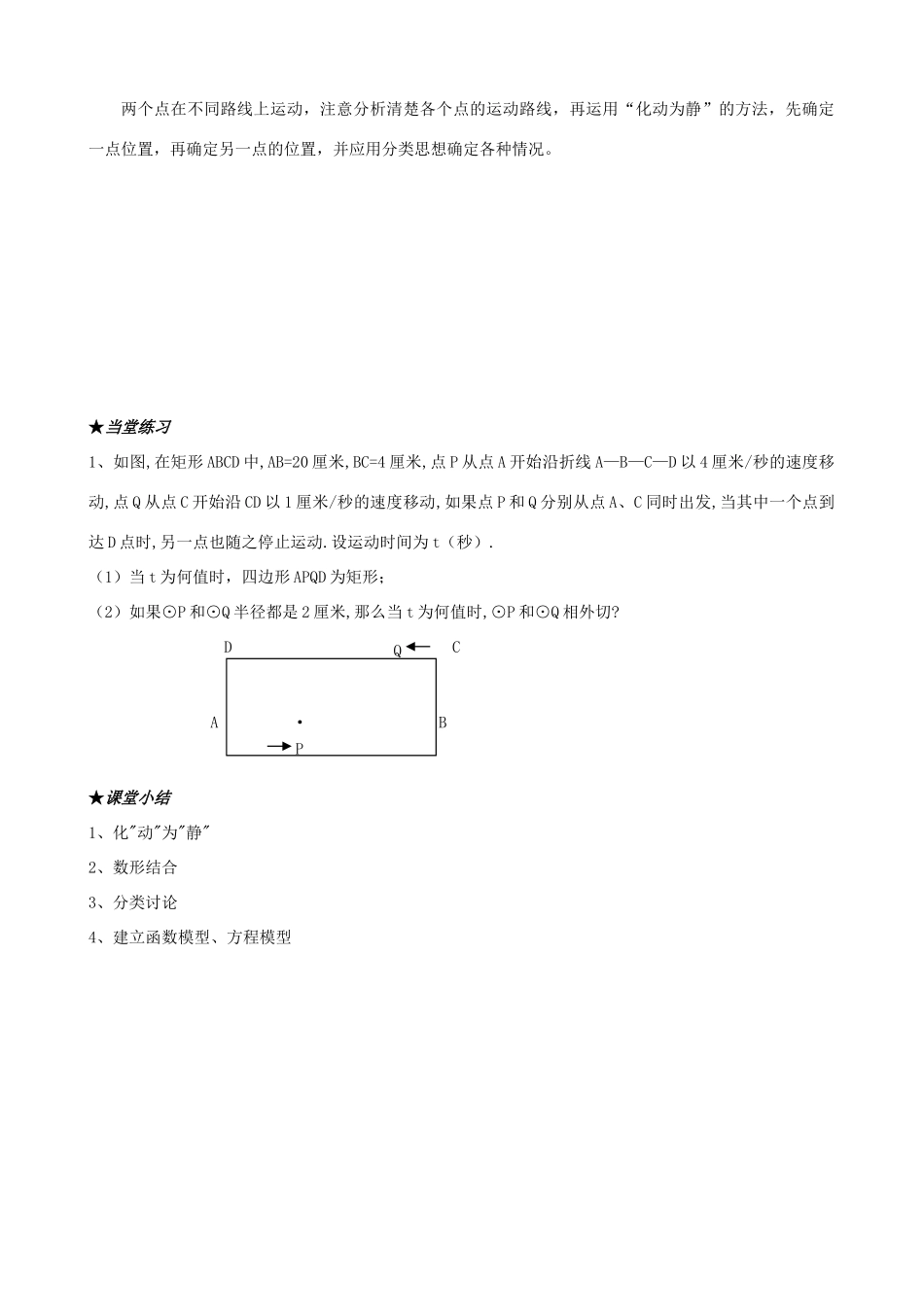
中考数学复习教案:动点问题【教学目标】1、知识目标:能够对点在运动变化过程中相伴随的数量关系、图形位置关系等进行观察研究。2、能力目标:进一步发展学生探究性学习能力,培养学生动手、动脑、手脑和谐一致的习惯。3、情感目标:培养浓厚的学习兴趣,养成与他人合作交流的习惯。【重点难点】1、教学重点:化“动”为“静”2、教学难点:运动变化过程中的数量关系、图形位置关系【教学方法】实践操作、引导探究【教学用具】多媒体、几何画板软件【教学过程】图形中的点、线的运动,构成了数学中的一个新问题——动态几何。它通常分为三种类型:动点问题、动线问题、动形问题。在解这类题时,要充分发挥空间想象的能力,往往不要被“动”所迷惑,而是要在“动”中求“静”,化“动”为“静”,抓住它运动中的某一瞬间,寻找确定的关系式,就能找到解决问题的途径。本节课来研究动态几何中的第一种类型——动点问题。动点问题主要研究点在直线上运动、点在圆上运动两种情况。点在直线上运动问题1:如图,在边长为4cm的正方形ABCD中,现有一动点P,从点A出发,以2cm/秒的速度,沿正方形的边经A-B-C-D到达点D。设运动时间为x秒。(1)当点P运动3.5秒时,点P到达什么位置?当点P运动秒时,点P到点A的距离为5cm;(2)连结始点A、动点P、终点D形成△APD,设其面积为S,求S与x的函数关系式;(3)如图,另有一动点Q,以1cm/秒的速度从点D出发,沿正方形的边经D-C-B到达点B,点P、Q分别从点A、D同时出发。连结AP、PQ、QA,设△PAQ的面积为W,试求在点P、Q相遇前,W与x之间的关系式。思路点拨:点在直线图形上运动,随着时间的变化,点的位置也会发生改变,与之相关的图形也在发生改变,所以解题时要分类讨论。根据点的运动情况,正确画出图形,思考时多画几张草图。在解第(3)小题时,有两个点在同时运动,而且运动的速度不同,要注意数形结合。点在曲线上运动问题2:如图,已知⊙O弦AB的长为60,点P是⊙O上的动点(P与A、B不重合),连结AP、BP。⑴若⊙O的半径为,求∠APB的度数;⑵若点P是优弧AB上的动点,∠APB的正切值为2,①若△APB为直角三角形,求PB的长;②若△APB为等腰三角形,求△APB的面积。思路点拨:点在曲线图形上运动,注意运用“化动为静”的方法,再用圆的性质等一些知识来解决。由于是动点,所以解题时要注意数形结合、分类讨论等数学思想的应用。两点复杂运动问题3:如图,抛物线与x轴交A、B两点(A点在B点左侧),直线与抛物线交于A、C两点,其中C点的横坐标为2.(1)求A、B、C三点的坐标;(2)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.思路点拨:两个点在不同路线上运动,注意分析清楚各个点的运动路线,再运用“化动为静”的方法,先确定一点位置,再确定另一点的位置,并应用分类思想确定各种情况。★当堂练习1、如图,在矩形ABCD中,AB=20厘米,BC=4厘米,点P从点A开始沿折线A—B—C—D以4厘米/秒的速度移动,点Q从点C开始沿CD以1厘米/秒的速度移动,如果点P和Q分别从点A、C同时出发,当其中一个点到达D点时,另一点也随之停止运动.设运动时间为t(秒).(1)当t为何值时,四边形APQD为矩形;(2)如果⊙P和⊙Q半径都是2厘米,那么当t为何值时,⊙P和⊙Q相外切?D·CA·B★课堂小结1、化"动"为"静"2、数形结合3、分类讨论4、建立函数模型、方程模型PQ