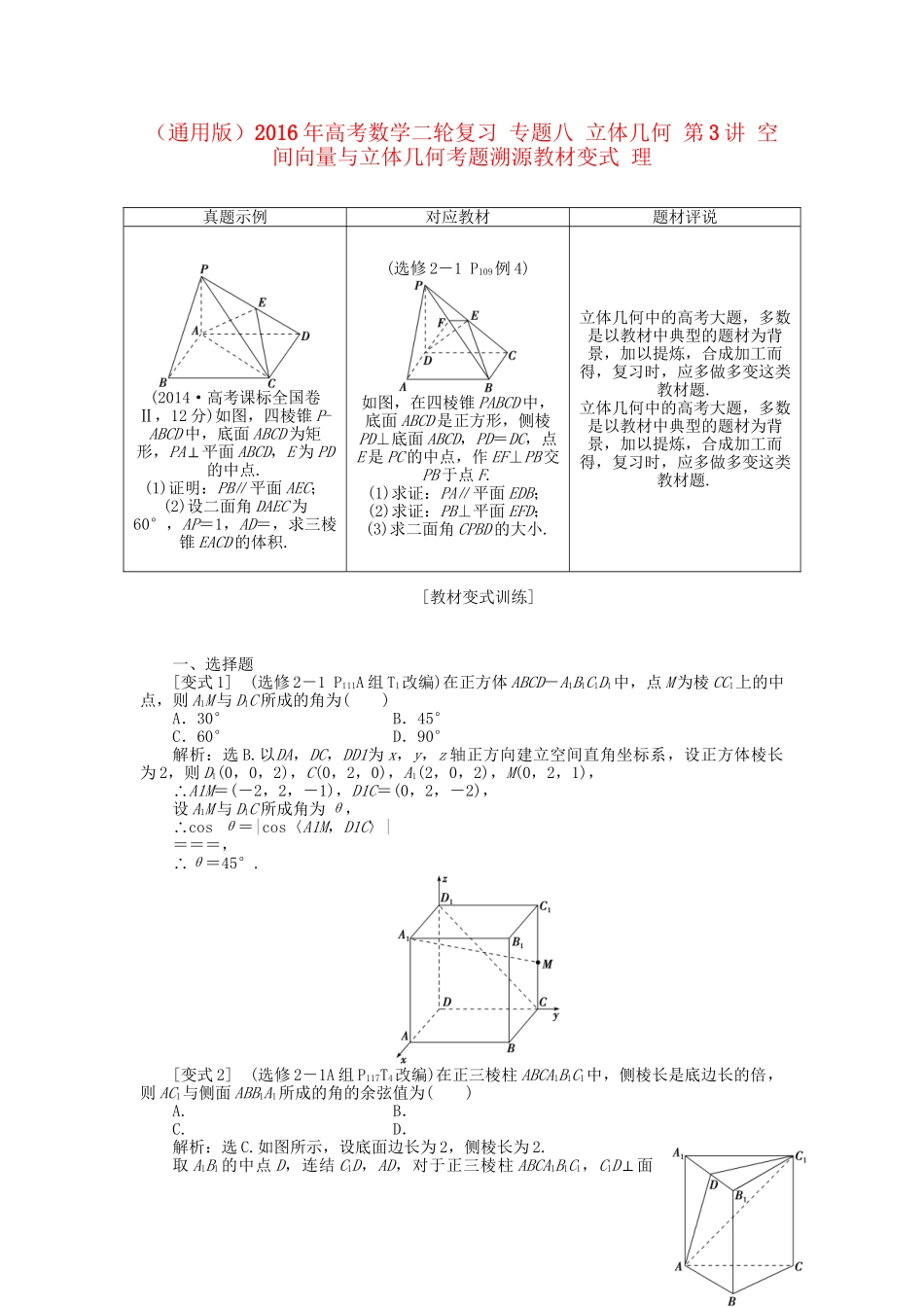
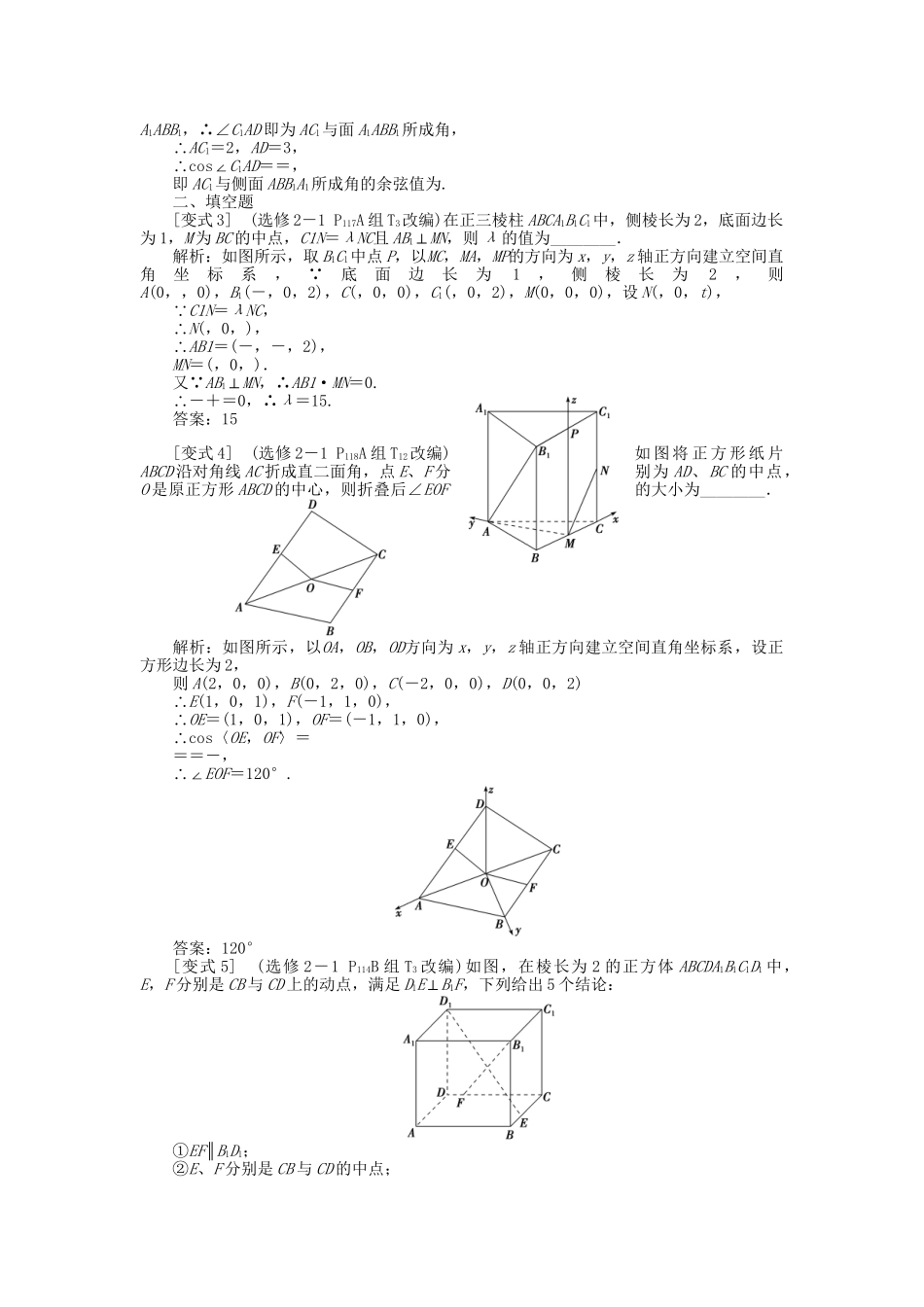
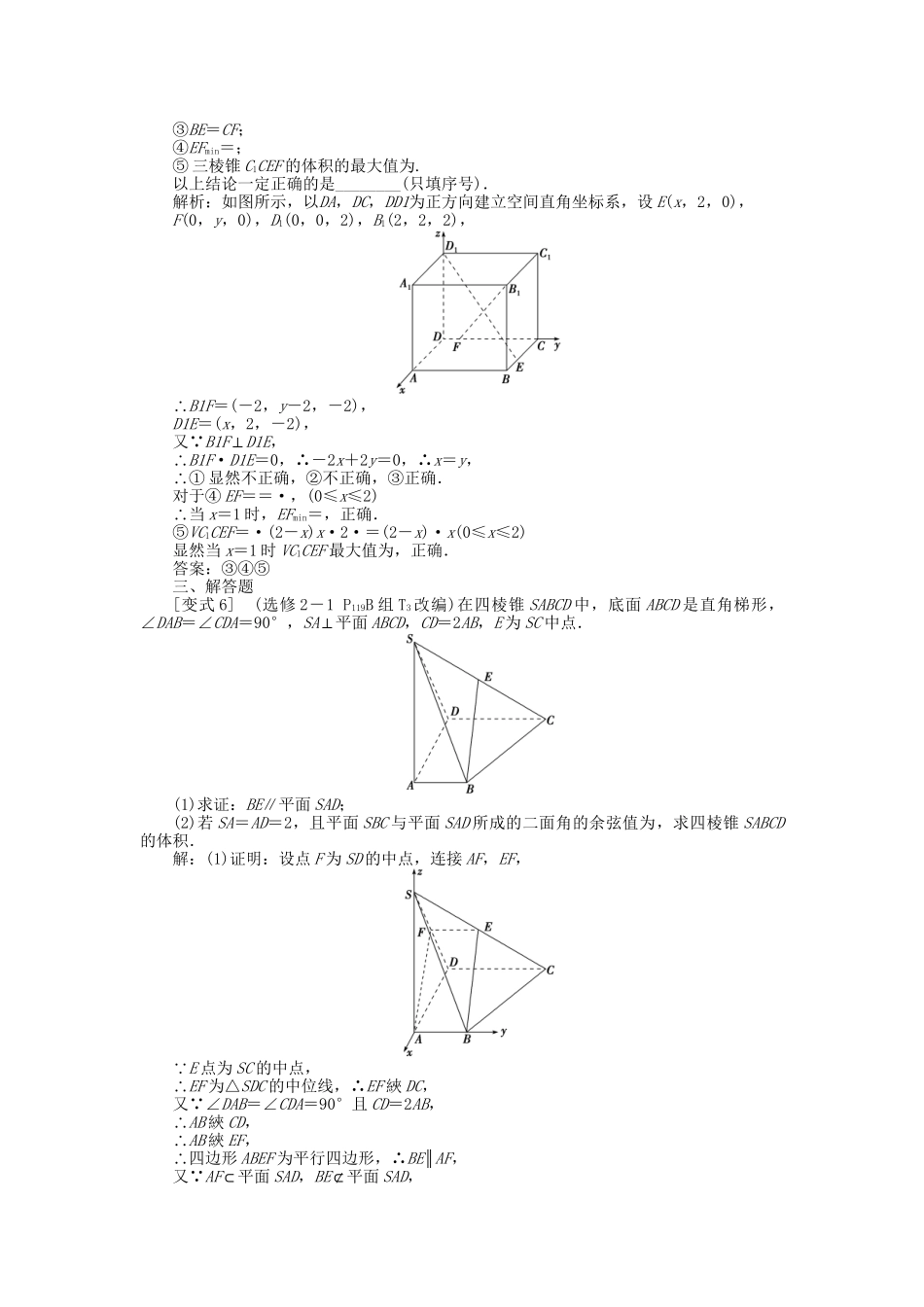
(通用版)2016年高考数学二轮复习专题八立体几何第3讲空间向量与立体几何考题溯源教材变式理真题示例对应教材题材评说(2014·高考课标全国卷Ⅱ,12分)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.(1)证明:PB∥平面AEC;(2)设二面角DAEC为60°,AP=1,AD=,求三棱锥EACD的体积.(选修2-1P109例4)如图,在四棱锥PABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,点E是PC的中点,作EF⊥PB交PB于点F.(1)求证:PA∥平面EDB;(2)求证:PB⊥平面EFD;(3)求二面角CPBD的大小.立体几何中的高考大题,多数是以教材中典型的题材为背景,加以提炼,合成加工而得,复习时,应多做多变这类教材题.立体几何中的高考大题,多数是以教材中典型的题材为背景,加以提炼,合成加工而得,复习时,应多做多变这类教材题.[教材变式训练]一、选择题[变式1](选修2-1P111A组T1改编)在正方体ABCD-A1B1C1D1中,点M为棱CC1上的中点,则A1M与D1C所成的角为()A.30°B.45°C.60°D.90°解析:选B.以DA,DC,DD1为x,y,z轴正方向建立空间直角坐标系,设正方体棱长为2,则D1(0,0,2),C(0,2,0),A1(2,0,2),M(0,2,1),∴A1M=(-2,2,-1),D1C=(0,2,-2),设A1M与D1C所成角为θ,∴cosθ=|cos〈A1M,D1C〉|===,∴θ=45°.[变式2](选修2-1A组P117T4改编)在正三棱柱ABCA1B1C1中,侧棱长是底边长的倍,则AC1与侧面ABB1A1所成的角的余弦值为()A.B.C.D.解析:选C.如图所示,设底面边长为2,侧棱长为2.取A1B1的中点D,连结C1D,AD,对于正三棱柱ABCA1B1C1,C1D⊥面A1ABB1,∴∠C1AD即为AC1与面A1ABB1所成角,∴AC1=2,AD=3,∴cos∠C1AD==,即AC1与侧面ABB1A1所成角的余弦值为.二、填空题[变式3](选修2-1P117A组T3改编)在正三棱柱ABCA1B1C1中,侧棱长为2,底面边长为1,M为BC的中点,C1N=λNC且AB1⊥MN,则λ的值为________.解析:如图所示,取B1C1中点P,以MC,MA,MP的方向为x,y,z轴正方向建立空间直角坐标系, 底面边长为1,侧棱长为2,则A(0,,0),B1(-,0,2),C(,0,0),C1(,0,2),M(0,0,0),设N(,0,t), C1N=λNC,∴N(,0,),∴AB1=(-,-,2),MN=(,0,).又 AB1⊥MN,∴AB1·MN=0.∴-+=0,∴λ=15.答案:15[变式4](选修2-1P118A组T12改编)如图将正方形纸片ABCD沿对角线AC折成直二面角,点E、F分别为AD、BC的中点,O是原正方形ABCD的中心,则折叠后∠EOF的大小为________.解析:如图所示,以OA,OB,OD方向为x,y,z轴正方向建立空间直角坐标系,设正方形边长为2,则A(2,0,0),B(0,2,0),C(-2,0,0),D(0,0,2)∴E(1,0,1),F(-1,1,0),∴OE=(1,0,1),OF=(-1,1,0),∴cos〈OE,OF〉===-,∴∠EOF=120°.答案:120°[变式5](选修2-1P114B组T3改编)如图,在棱长为2的正方体ABCDA1B1C1D1中,E,F分别是CB与CD上的动点,满足D1E⊥B1F,下列给出5个结论:①EF∥B1D1;②E、F分别是CB与CD的中点;③BE=CF;④EFmin=;⑤三棱锥C1CEF的体积的最大值为.以上结论一定正确的是________(只填序号).解析:如图所示,以DA,DC,DD1为正方向建立空间直角坐标系,设E(x,2,0),F(0,y,0),D1(0,0,2),B1(2,2,2),∴B1F=(-2,y-2,-2),D1E=(x,2,-2),又 B1F⊥D1E,∴B1F·D1E=0,∴-2x+2y=0,∴x=y,∴①显然不正确,②不正确,③正确.对于④EF==·,(0≤x≤2)∴当x=1时,EFmin=,正确.⑤VC1CEF=·(2-x)x·2·=(2-x)·x(0≤x≤2)显然当x=1时VC1CEF最大值为,正确.答案:③④⑤三、解答题[变式6](选修2-1P119B组T3改编)在四棱锥SABCD中,底面ABCD是直角梯形,∠DAB=∠CDA=90°,SA⊥平面ABCD,CD=2AB,E为SC中点.(1)求证:BE∥平面SAD;(2)若SA=AD=2,且平面SBC与平面SAD所成的二面角的余弦值为,求四棱锥SABCD的体积.解:(1)证明:设点F为SD的中点,连接AF,EF, E点为SC的中点,∴EF为△SDC的中位线,∴EF綊DC,又 ∠DAB=∠CDA=90°且CD=2AB,∴AB綊CD,∴AB綊EF,∴四边形ABEF为平行四边形,∴BE∥AF,又 AF⊂平面SAD,BE⊄平面SAD,∴BE∥平面SAD.(2...